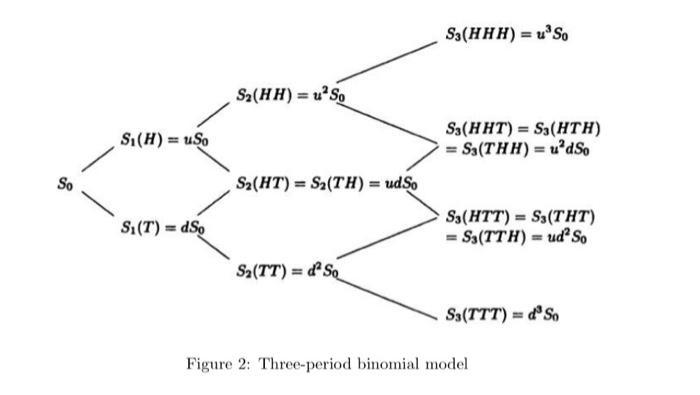
2. Consider a three-period binomial model in Figure 2 with So 4, u = 2, and d = risk-free rate is 10% at each period. The payoff of the focus asset is S3. = = 1/2. The (a) What is the no-arbitrage price of V(H)? (b) How many shares of stock should one hold in the replicated portfolio X(H)? (c) What is the risk-neutral distribution of S3 (S = S (H)), i.e., the condition distribution S (H) under the risk-neutral measure? of S3 given S (d) Based on the conditional distribution that you obtained in 2(c), compute [V3|(S = S(H))]. What can you find by comparing your result with that in 2(a)? So S (H) = uso S1 (T)=dSo S2(HH)=uSo S2(HT) = S(TH) = udSo S2(TT)= d'So S3(HHH)=uSo S3(HHT) = S3(HTH) = S3(THH)=udSo S3(HTT) = S(THT) = S3(TTH) = ud So S3(TTT)=d So Figure 2: Three-period binomial model. 2. Consider a three-period binomial model in Figure 2 with So 4, u = 2, and d = risk-free rate is 10% at each period. The payoff of the focus asset is S3. = = 1/2. The (a) What is the no-arbitrage price of V(H)? (b) How many shares of stock should one hold in the replicated portfolio X(H)? (c) What is the risk-neutral distribution of S3 (S = S (H)), i.e., the condition distribution S (H) under the risk-neutral measure? of S3 given S (d) Based on the conditional distribution that you obtained in 2(c), compute [V3|(S = S(H))]. What can you find by comparing your result with that in 2(a)? So S (H) = uso S1 (T)=dSo S2(HH)=uSo S2(HT) = S(TH) = udSo S2(TT)= d'So S3(HHH)=uSo S3(HHT) = S3(HTH) = S3(THH)=udSo S3(HTT) = S(THT) = S3(TTH) = ud So S3(TTT)=d So Figure 2: Three-period binomial model.