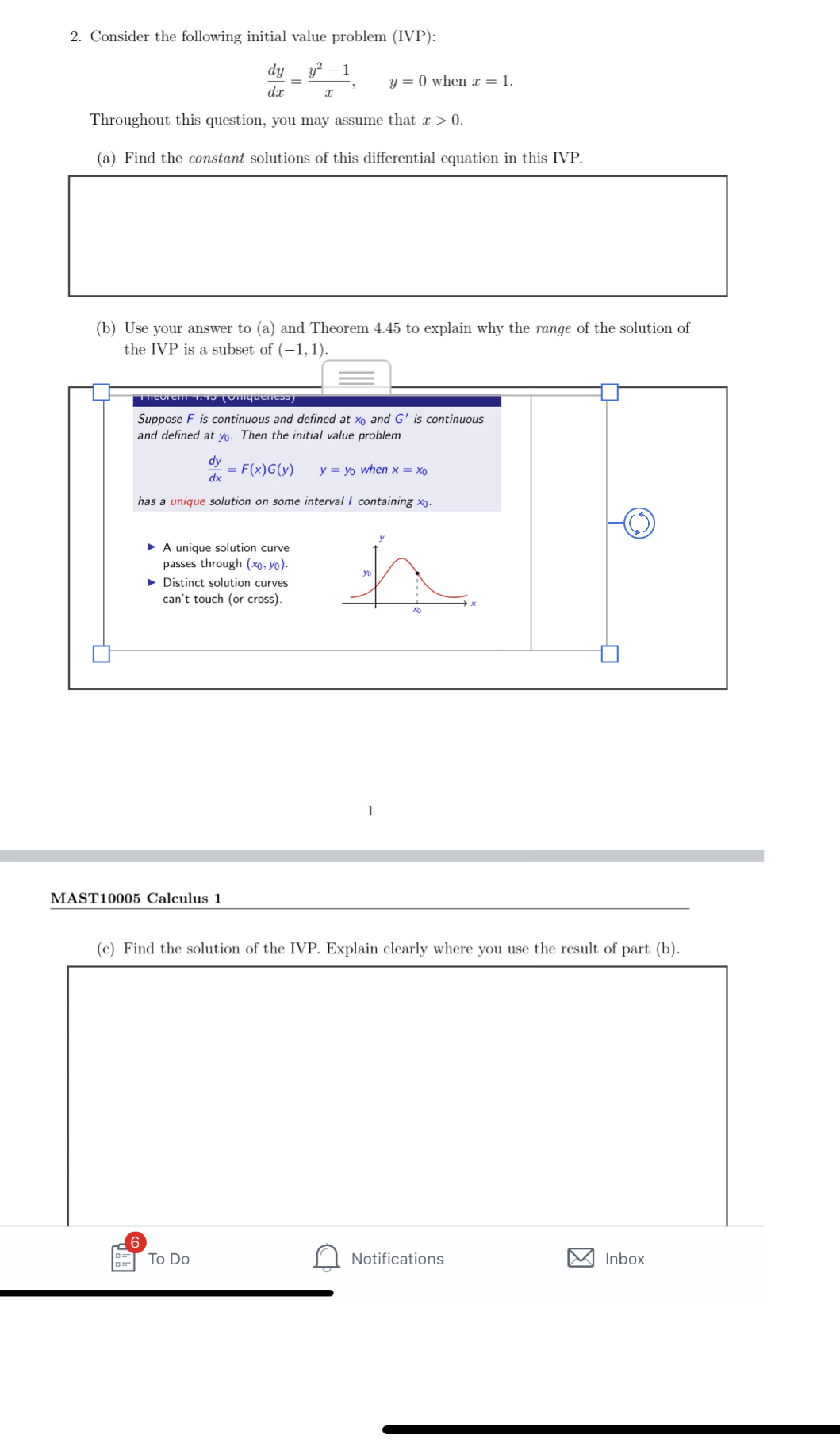
2. Consider the following initial value problem (IVP): dy y2 - 1 dx y = 0 when x = 1. Throughout this question, you may assume that I > 0. (a) Find the constant solutions of this differential equation in this IVP. (b) Use your answer to (a) and Theorem 4.45 to explain why the range of the solution of the IVP is a subset of (-1, 1). Suppose F is continuous and defined at xo and G' is continuous and defined at yo. Then the initial value problem dx dy = F (x ) G (y ) y = yo when x = Xo has a unique solution on some interval I containing xo. A unique solution curve passes through (x0, yo)- Distinct solution curves can't touch (or cross) MAST10005 Calculus 1 (c) Find the solution of the IVP. Explain clearly where you use the result of part (b). 6 To Do Notifications Inbox(d) Prove that your answer to part (c) is a solution of the IVP. Don't forget to verify the initial condition. Assignment Information This assignment is worth 29% of your final MAST10005 mark. There will be 1 mark overall for correct mathematical notation. Solutions will be uploaded to Canvas approximately 3 days after the deadline. 3 6 To Do Notifications Inbox