2. Define f to be (x + 3)2 - 2.The next two steps are used to invert f(x) so that you obtain an expression for x as a function of y. You will then use this to calculate the area of a infinitesimally thin disc obtained by cutting a slice through the solid at a fixed value of y. The area of the disc can then be integrated over y to obtain the volume of the solid.3. Define g to be y - f.4. Use the function solve(g?x) to obtain an expression for x in terms of y. (The output line will just be an expression in terms of y).5. Calculate the area of an infinitesimally thin disc of the solid perpendicular to the y axis as a function of y.6. Using the int function, integrate the expression you got for the disc area in Step 5 over y, to obtain the volume of the solid.7. Convert the answer you obtained in Step 6 to a decimal number by using the evalf function.

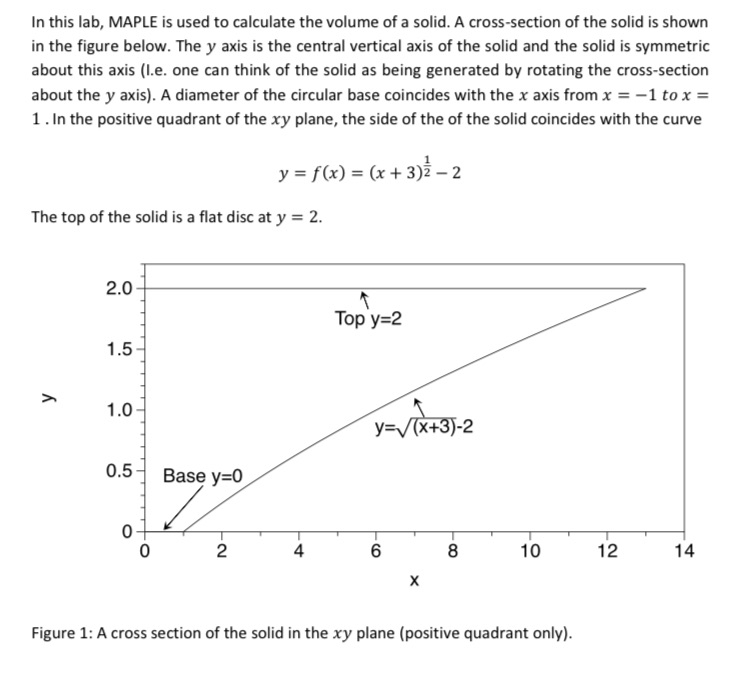
In this lab, MAPLE is used to calculate the volume of a solid. A cross-section of the solid is shown in the figure below. The y axis is the central vertical axis of the solid and the solid is symmetric about this axis (l.e. one can think of the solid as being generated by rotating the cross-section about the y axis). A diameter of the circular base coincides with the x axis from x = -1 to x = 1 . In the positive quadrant of the xy plane, the side of the of the solid coincides with the curve y = f (x) = (x+3)2-2 The top of the solid is a flat disc at y = 2. 2.0 Top y=2 1.5 1.0 y=(x+3)-2 0.5- Base y=0 2 6 8 10 12 14 X Figure 1: A cross section of the solid in the xy plane (positive quadrant only)