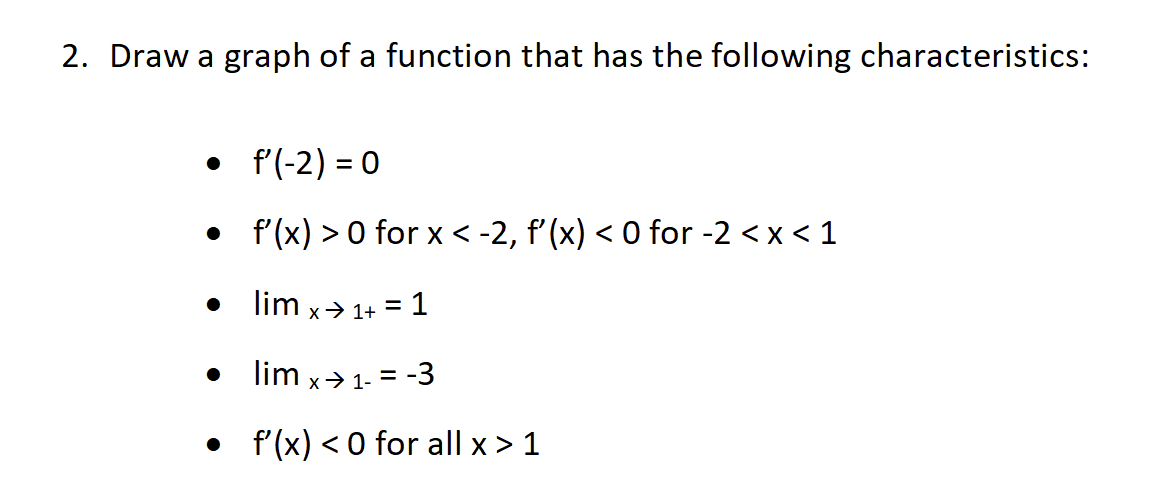
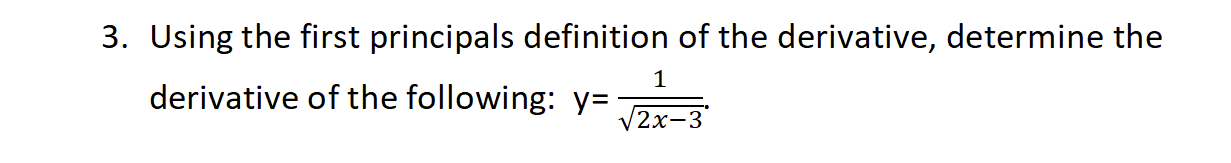
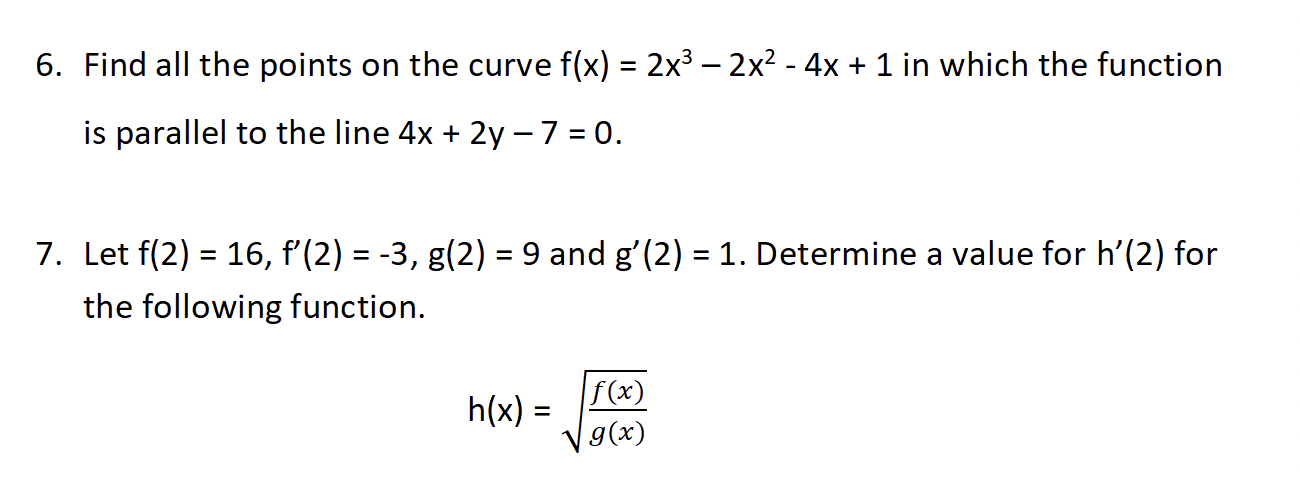
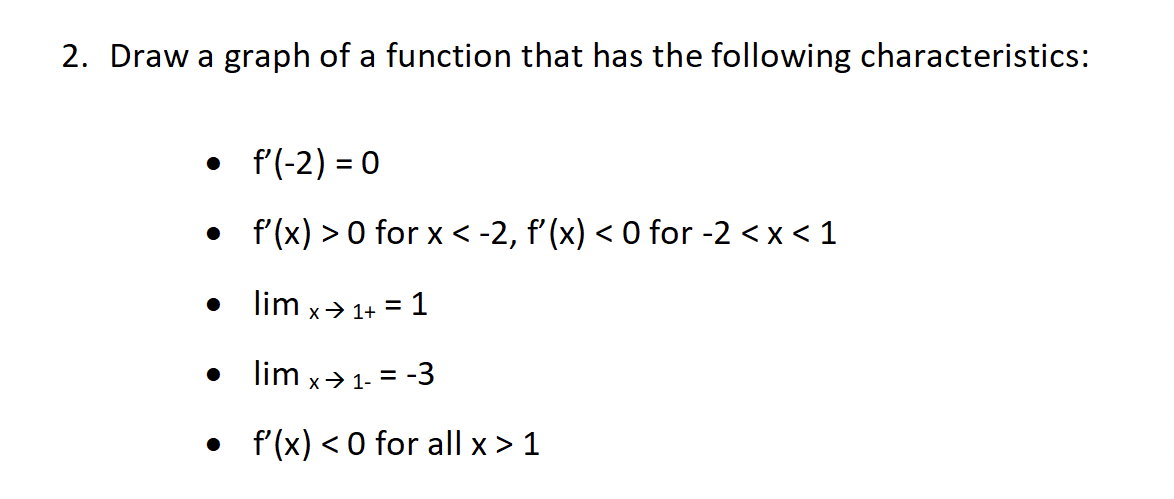
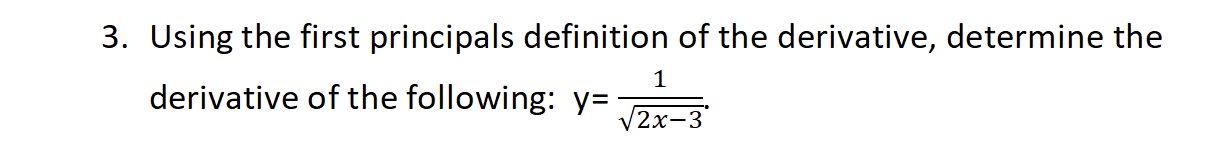
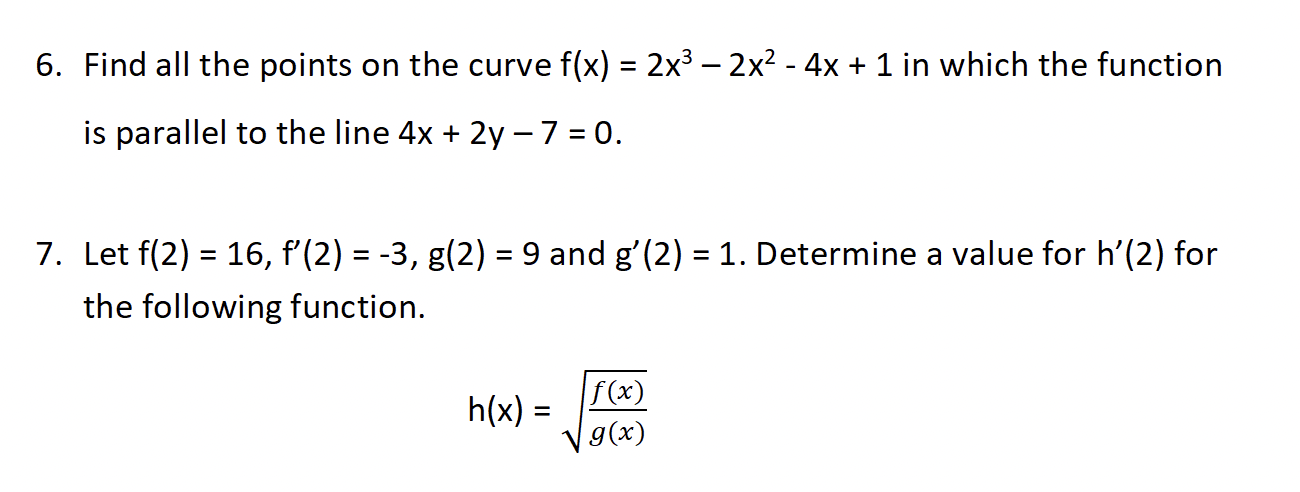
2. Draw a graph of a function that has the following characteristics: . f' ( -2) = 0 . f'(x) > 0 for x 13. Using the first principals definition of the derivative, determine the 1 vzx3' derivative of the following: y: 5. Find the equation of the tangent line to the function y = 2(x3 2x)4 at the point x = 1. 6. Find all the points on the curve f(x) = 2x3 2x2 - 4x + 1 in which the function is parallel to the line 4x + 2y 7 = 0. 7. Let f(2) = 16, f'(2) = -3, g(2) = 9 and g'(2) = 1. Determine a value for h'(2) for the following function. f(x) h = lxl gov)