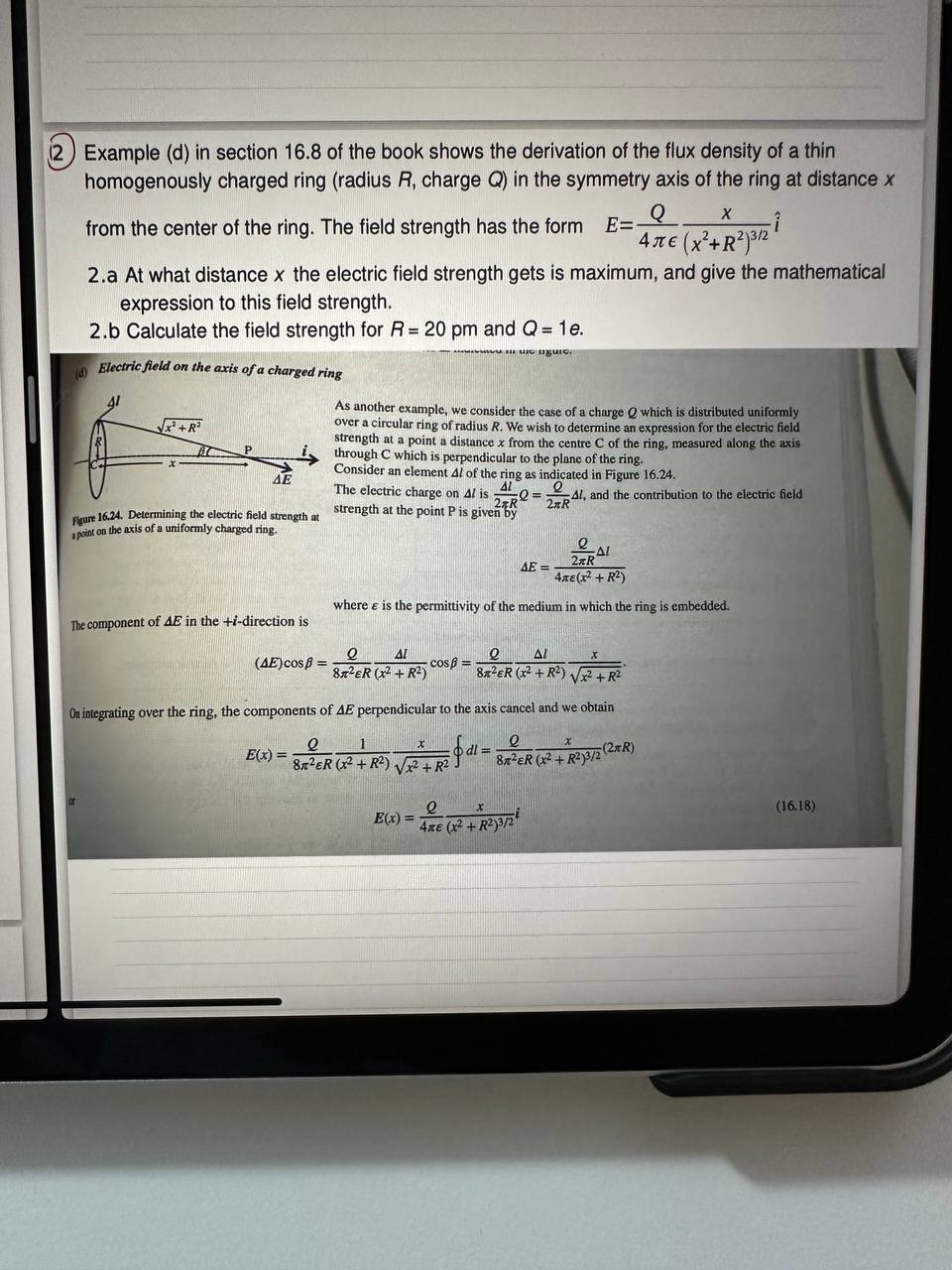
(2) Example (d) in section 16.8 of the book shows the derivation of the flux density of a thin homogenously charged ring (radius R, charge Q) in the symmetry axis of the ring at distance x Q X 4 (x+R)/2 213/2 2.a At what distance x the electric field strength gets is maximum, and give the mathematical expression to this field strength. 2.b Calculate the field strength for R= 20 pm and Q = 1e. uno siguien Electric field on the axis of a charged ring 41 from the center of the ring. The field strength has the form E=- x+R Figure 16.24. Determining the electric field strength at a point on the axis of a uniformly charged ring. The component of AE in the +i-direction is (AE) cos = As another example, we consider the case of a charge Q which is distributed uniformly over a circular ring of radius R. We wish to determine an expression for the electric field strength at a point a distance x from the centre C of the ring, measured along the axis through C which is perpendicular to the plane of the ring. Consider an element Al of the ring as indicated in Figure 16.24. The electric charge on Al is=; strength at the point P is given by AL 0 244, and the contribution to the electric field E(x) = AL 2xR 4Re (x + R) where & is the permittivity of the medium in which the ring is embedded. e Al 8ER (x+R)x + R +R On integrating over the ring, the components of AE perpendicular to the axis cancel and we obtain 32ER (x + R233/20 Q Al 87ER (x + R) cos= O 1 8ER (x+R)x + R E(x) = dl= AE= 2 4xe (x + R)3/2 -(2xR) (16.18)