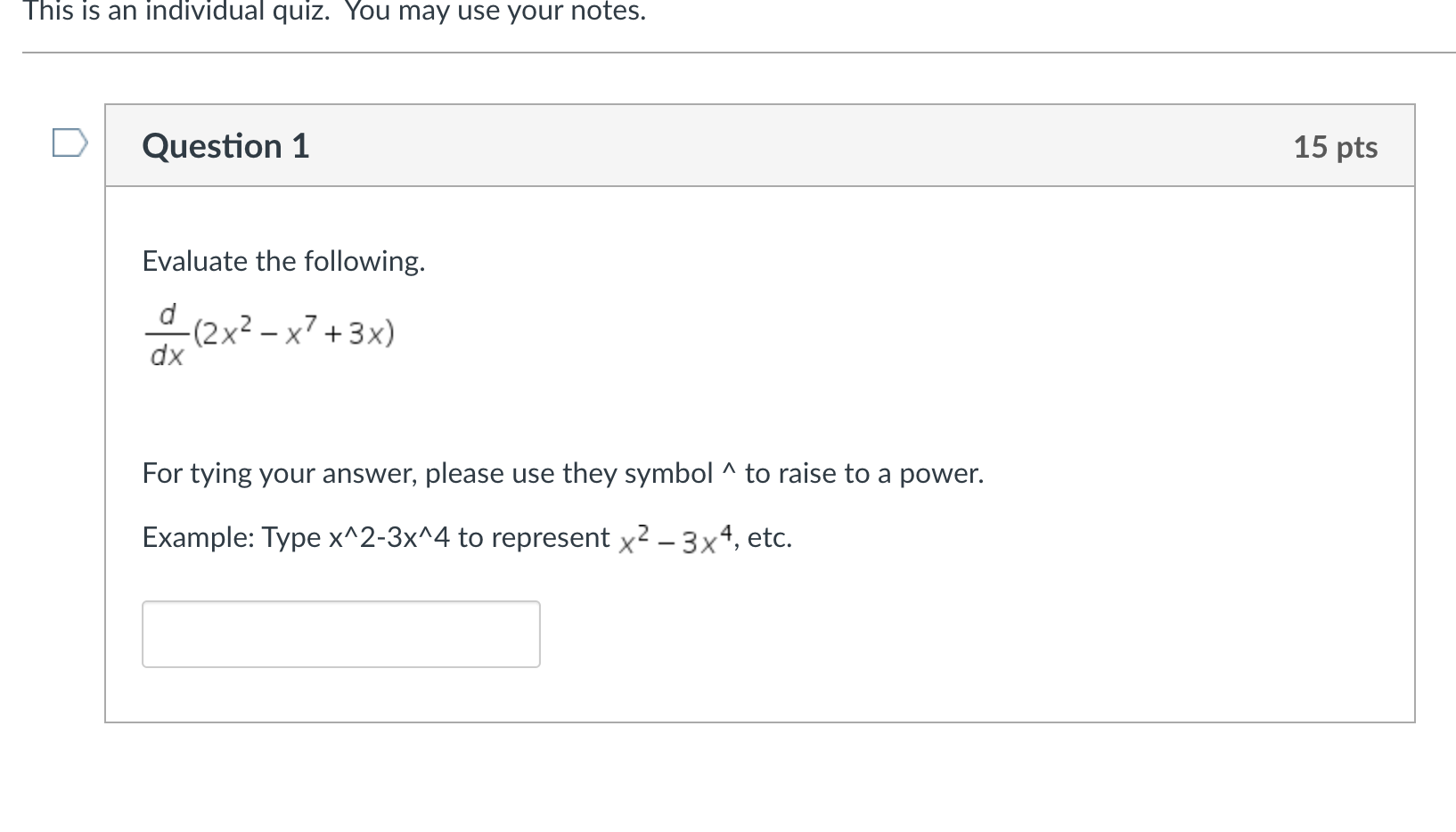
2. Examples of finding a derivative using the summation and constant multiple rules a. Here is the summation rule. SUMMATION RULE: "[f (x ) + g(x)]= [f(x)]+ -[g(x)] dx dx Or may be written... [f (x) + g(x)]' =f'(x)+ g'(x) Hence, we could find the derivative of a summation of functions. b. Written example. Find the derivative. h (x) = x2 + x10+5. h' ( x ) = [x2 ] + [x10]+ d dx dx -[5] dx h' (x) = 2x+ 10x9+0 Conclusion: h'(x ) = 2x+ 10x9c. Here is the constant multiple rule. CONSTANT MULTIPLE RULE: dx "[C . f ( x) ] = C- [f (x)] Or may be written... [c . f(x)]' = C.[f(x)]' Hence, we could find the derivative of any constant multiple of a function. d. Written example. Find the derivative. h(x) =. 5 x 2 h' ( x ) = d 5 d dx dx =5- [x-2]=5[-2x-2-1]= - 10x-3_ _ 10 Conclusion: h' ( x ) = - 10 x33. Lab problems. (Continued in the next page) Use the rule above to find the derivatives. 6. Find f' (x) if f(x) = - x 5 - x 5 . 7. Find -[16x7/4 ].2. Examples of finding a derivative using all the rules so far. a. Written example using power, summation, and the constant multiple rules. Find the derivative. g(x) =3x5/3 -6x3 + 99. g'(x) = -[3x5/3] _ [6x3]+ d [99] USING SUMMATION RULE dx dx dx g'(x) = 3 [x5/3]-6-d [x 3 ] + d dx dx [99] USING CONSTANT MULTIPLE RULE dx g'(x) = 3- 5 x2/3-6. 3x2 + 0 USING POWER RULE AND DERIVATIVE OF A CONSTANT W Conclusion: g'(x) =5x2/3 - 18x23. Lab problems. Use the rule above to find the derivatives. 8. Find f'(x) if f(x) = 5x4 - 3x. 9. Find [12 - 3x9 ]. dx 12 10. Find f'(x) if f(x) = - 6x1/2 X3/4This is an individual quiz. You may use your notes. D Question 1 15 pts Evaluate the following. For tying your answer, please use they symbol A to raise to a power. Example: Type x"2-3x"4 to represent x2 _ 3x4, etc