Question: 2. Find the logistic function that satisfies the given conditions: Initial value equals=11, limit to growth equals=33, passing through (4,20).3. Evaluate the following definite integral:
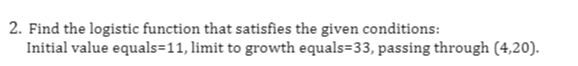
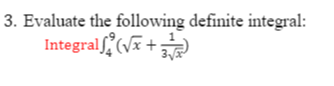
![definite integral: Integral(vx +])4. Write the expression as a single logarithm assuming](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66634ff00ce8a_55966634fefebcba.jpg)


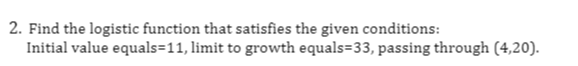
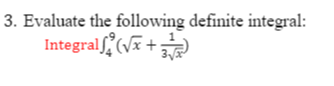



2. Find the logistic function that satisfies the given conditions: Initial value equals=11, limit to growth equals=33, passing through (4,20).3. Evaluate the following definite integral: Integral(vx +])4. Write the expression as a single logarithm assuming that x, y, and z are positive numbers log, 25 - log4 x - -logy - log4(z + 9)Identify the center, vertices, co-vertices, foci, length of the major axis, length of the minor axis, length of the latus rectum. 7) 3x2 + 35y' - 60x + 140y - 85 = 0Note: for the below question, the latus rectum is the focal length Identify the vertex, focus, axis of symmetry, directrix, direction of opening, min/max value length of the latus rectum, and the x- and y-intercepts of each. 7) -2x2 - 4x + y +70=0
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


