2)

For B, All values are not 0.9 or 90%, it is 95% or 0.95

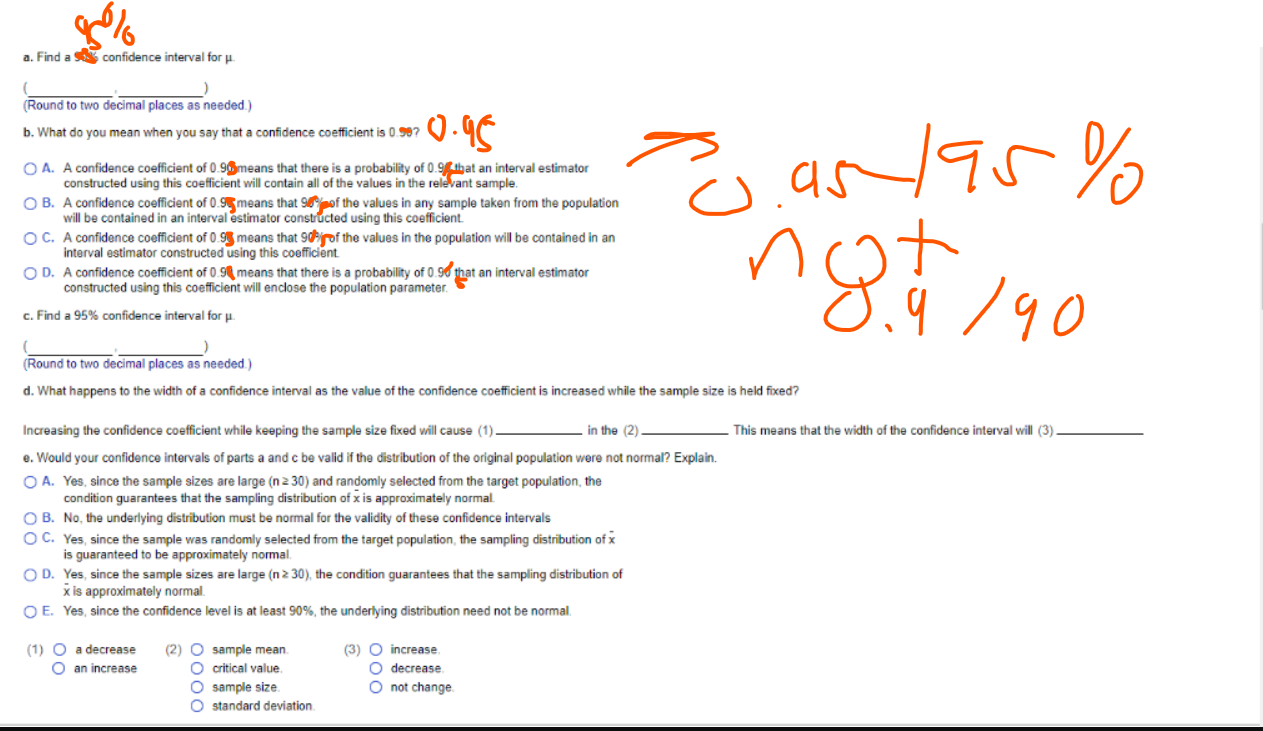
a. Find a 50 confidence interval for u (Round to two decimal places as needed.) b. What do you mean when you say that a confidence coefficient is 0.597 0.95 O A. A confidence coefficient of 0.905means that there is a probability of 0.9/that an interval estimator constructed using this coefficient will contain all of the values in the relevant sample. C O B. A confidence coefficient of 0.9% means that 9ty of the values in any sample taken from the population will be contained in an interval estimator constructed using this coefficient O C. A confidence coefficient of 0.9 means that 90 y of the values in the population will be contained in an interval estimator constructed using this coefficient O D. A confidence coefficient of 0.9% means that there is a probability of 0.90 that an interval estimator constructed using this coefficient will enclose the population parameter. C. Find a 95% confidence interval for u J. 9 / 90 (Round to two decimal places as needed.) d. What happens to the width of a confidence interval as the value of the confidence coefficient is increased while the sample size is held fixed? Increasing the confidence coefficient while keeping the sample size fixed will cause (1). - in the (2) - This means that the width of the confidence interval will (3) e. Would your confidence intervals of parts a and c be valid if the distribution of the original population were not normal? Explain. O A. Yes, since the sample sizes are large (n 2 30) and randomly selected from the target population, the condition guarantees that the sampling distribution of x is approximately normal. O B. No, the underlying distribution must be normal for the validity of these confidence intervals O C. Yes, since the sample was randomly selected from the target population, the sampling distribution of x is guaranteed to be approximately normal O D. Yes, since the sample sizes are large (n 2 30), the condition guarantees that the sampling distribution of x is approximately normal. O E. Yes, since the confidence level is at least 90%, the underlying distribution need not be normal. (1) O a decrease (2) O sample mean (3) O increase. O an increase O critical value O decrease sample size O not change. O standard deviation.A random sample of 100 observations from a normally distributed population possesses a mean equal to 85.7 and a standard deviation equal to 6.1. Use this information to complete parts a through e below. a. Find a 95% confidence interval for p. (Round to two decimal places as needed.)