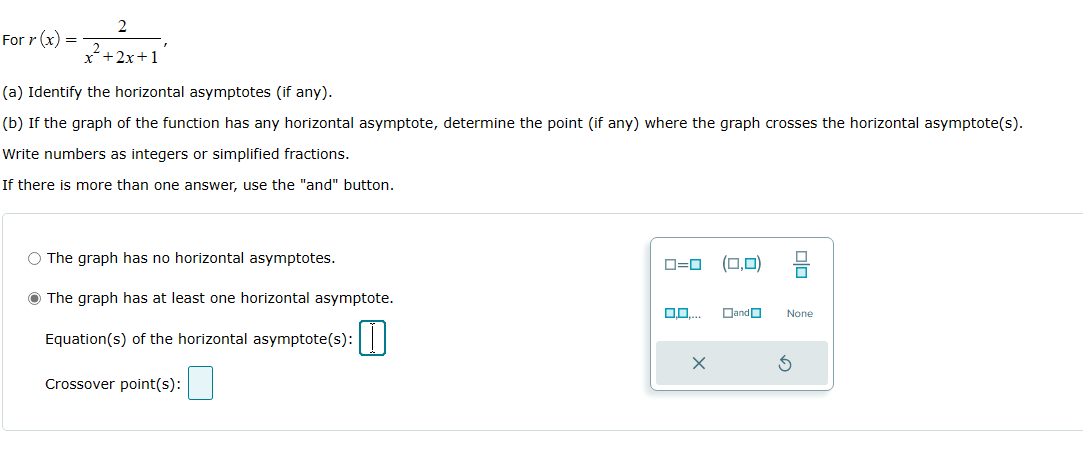
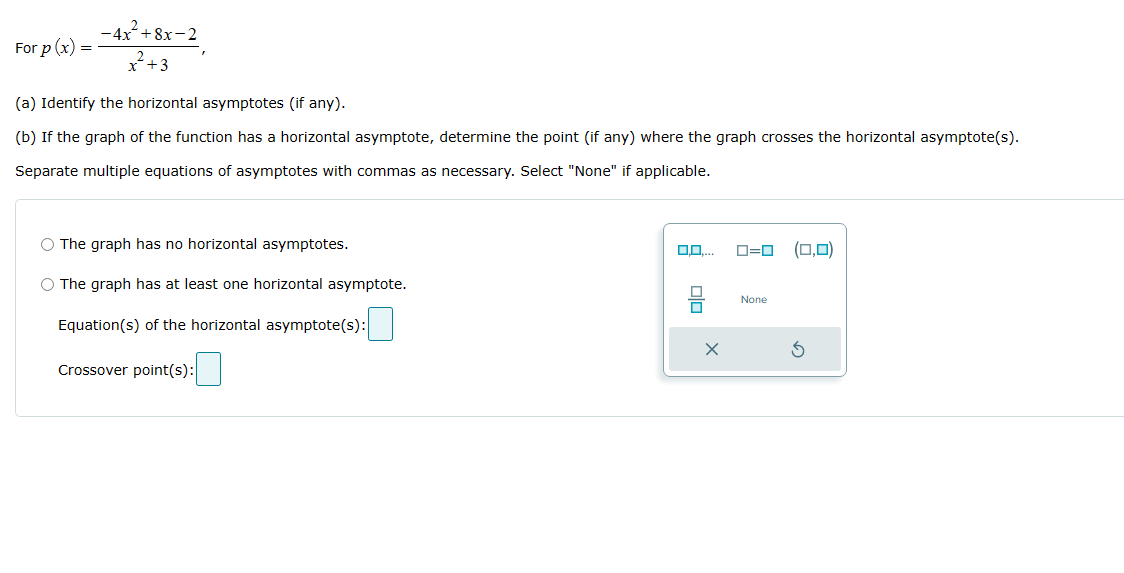
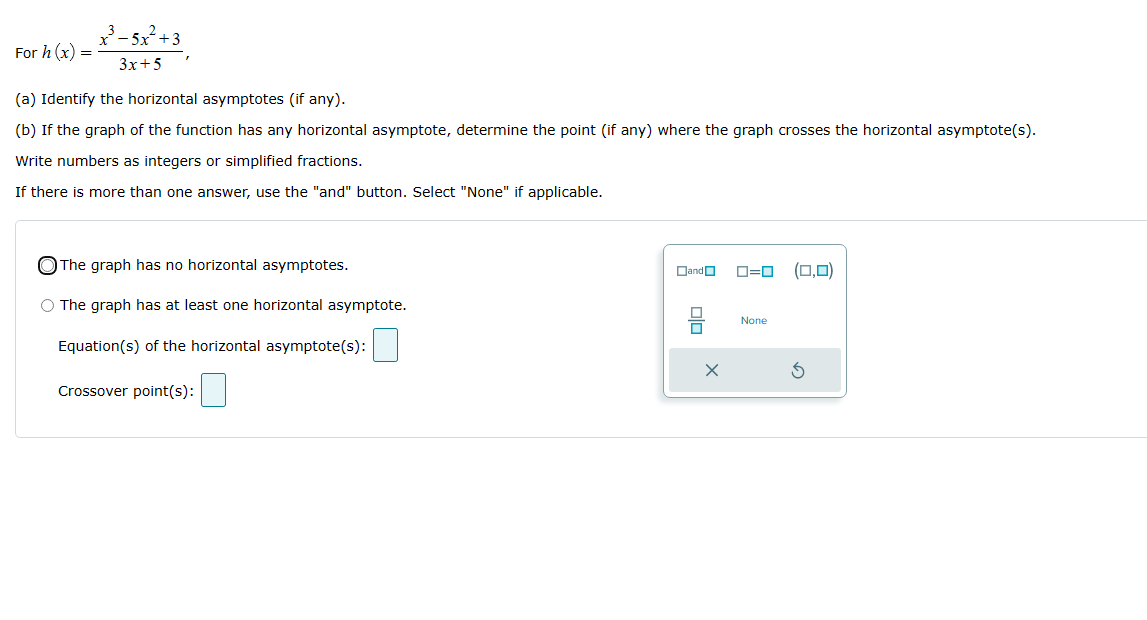
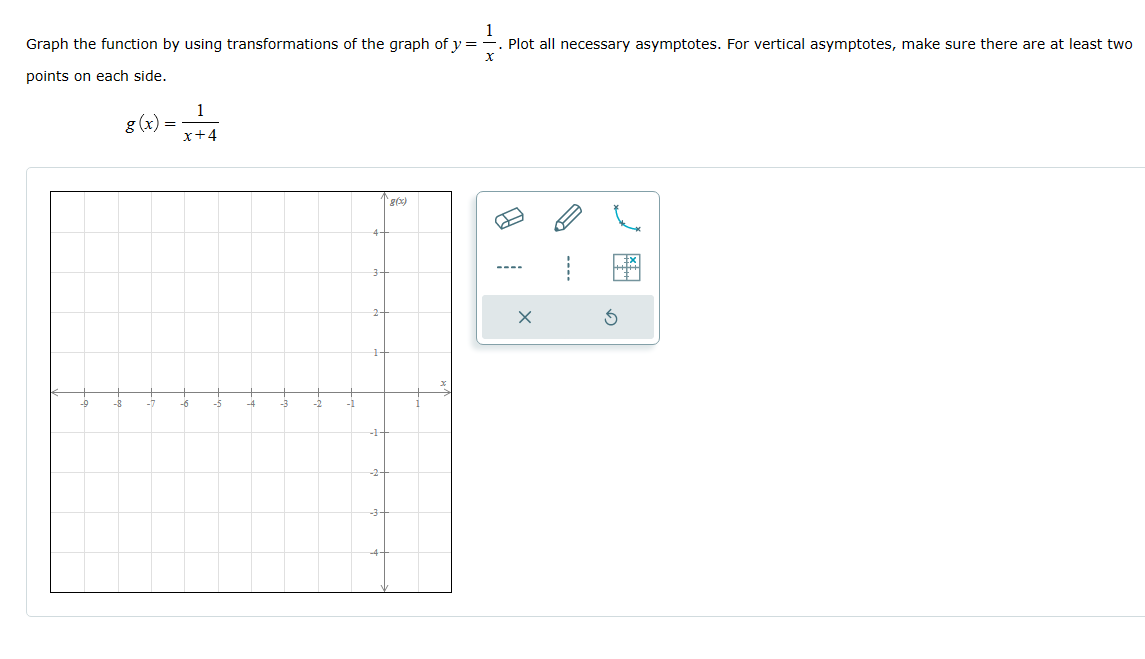
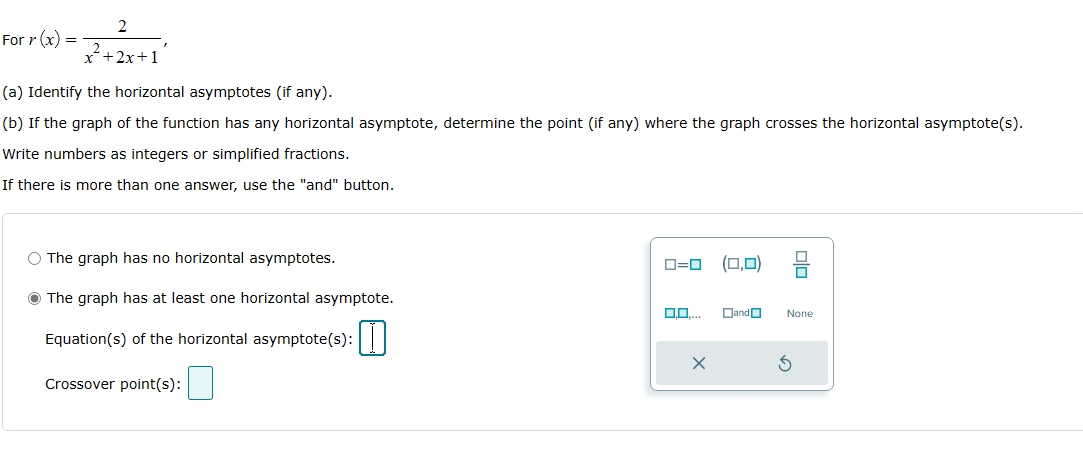
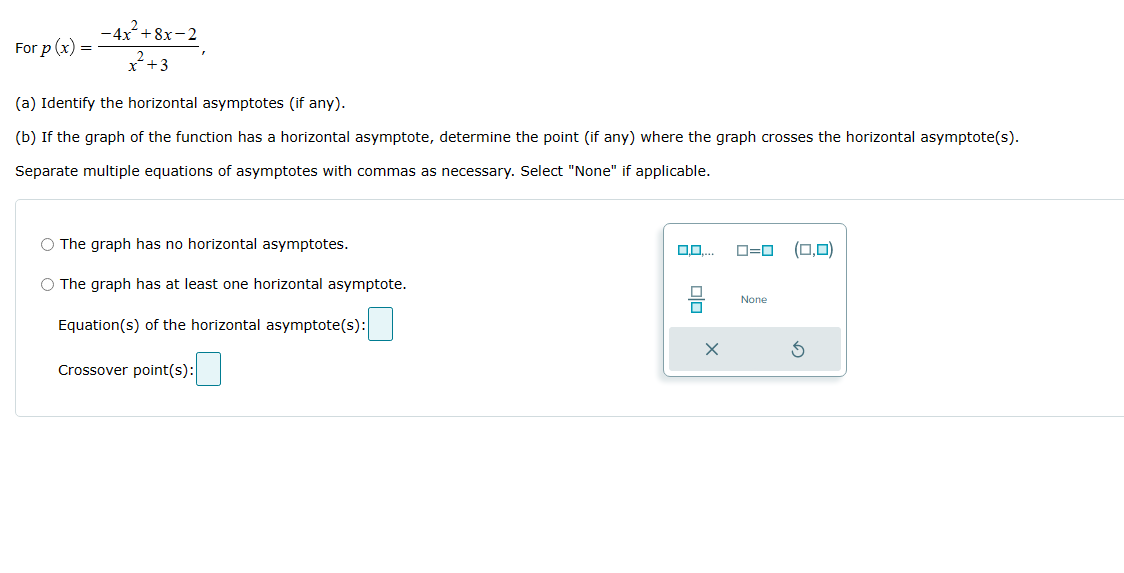
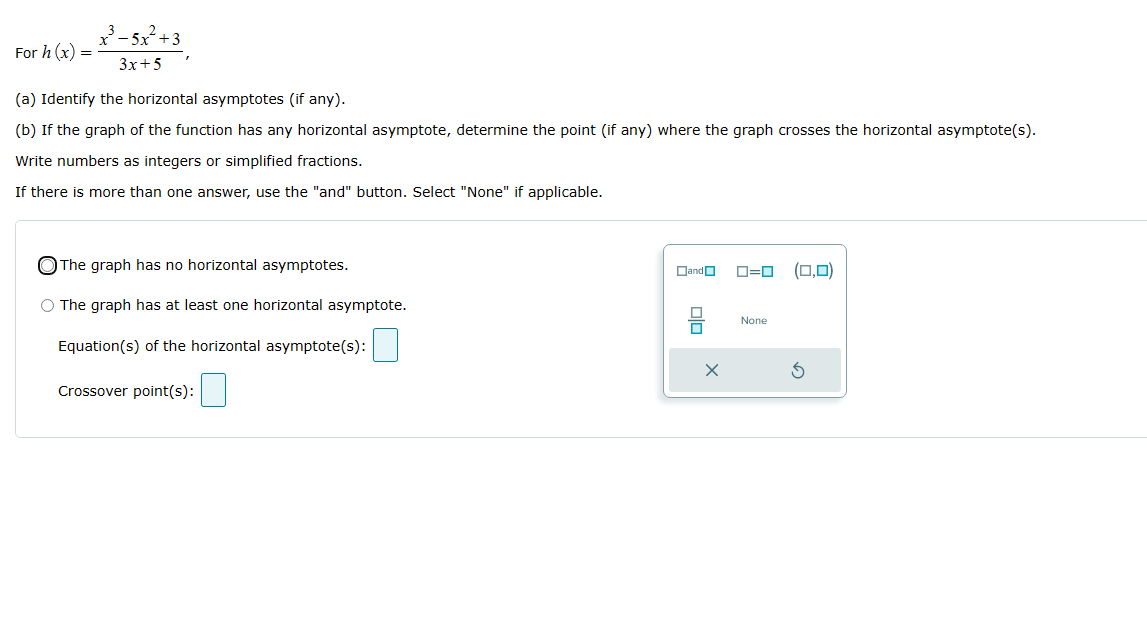
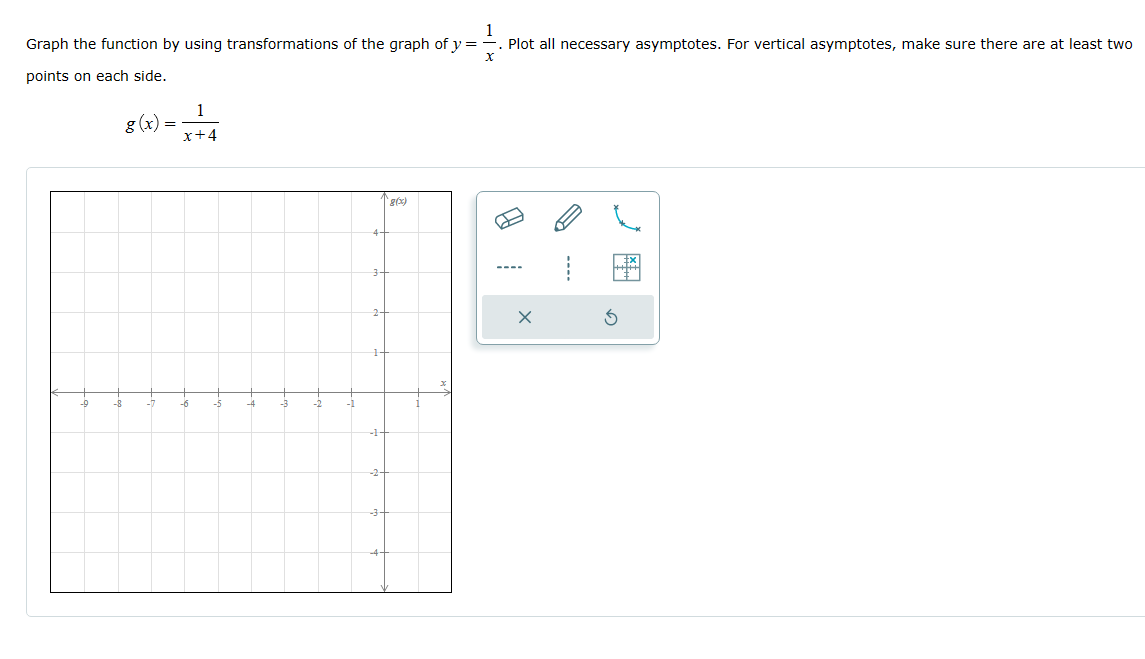
2 For r (x) = x'+2x+1 (a) Identify the horizontal asymptotes (if any). (b) If the graph of the function has any horizontal asymptote, determine the point (if any) where the graph crosses the horizontal asymptote(s). Write numbers as integers or simplified fractions. If there is more than one answer, use the "and" button. O The graph has no horizontal asymptotes. 0=0 (0,0) 0 O The graph has at least one horizontal asymptote. 0,0.... OJand None Equation(s) of the horizontal asymptote(s) X 5 Crossover point(S):-4x-+8x-2 For p (x) = 2 + 3 (a) Identify the horizontal asymptotes (if any). (b) If the graph of the function has a horizontal asymptote, determine the point (if any) where the graph crosses the horizontal asymptote(s). Separate multiple equations of asymptotes with commas as necessary. Select "None" if applicable. O The graph has no horizontal asymptotes. 0.0.... 0=0 (0,0) O The graph has at least one horizontal asymptote. None Equation(s) of the horizontal asymptote(s) : X 5 Crossover point(s) :F 1H) x35x2+3 or x = , 3x+ 5 (a) Identify the horizontal asymptotes (if any). (b) If the graph of the function has anyr horizontal asymptote, determine the point (if any) where the graph crosses the horizontal asymptote(s). Write numbers as integers or simplified fractions. If there is more than one answer, use the \"and" button. Select "None" if applicable. ."he graph has no horizontal asymptotes. HE] _ { ,D} "'22- "he graph has at least one horizontal asymptote. Nci'e Equation(s) of the horizontal asymptote(s): |:| Crossover point(s): |:| points on each side. X Graph the function by using transformations of the graph of y = -. Plot all necessary asymptotes. For vertical asymptotes, make sure there are at least two g ( x) = x+4 4- 3- 2- X 5 1- -8 -6 -5 -4 -2 -1 -1- -2- -3