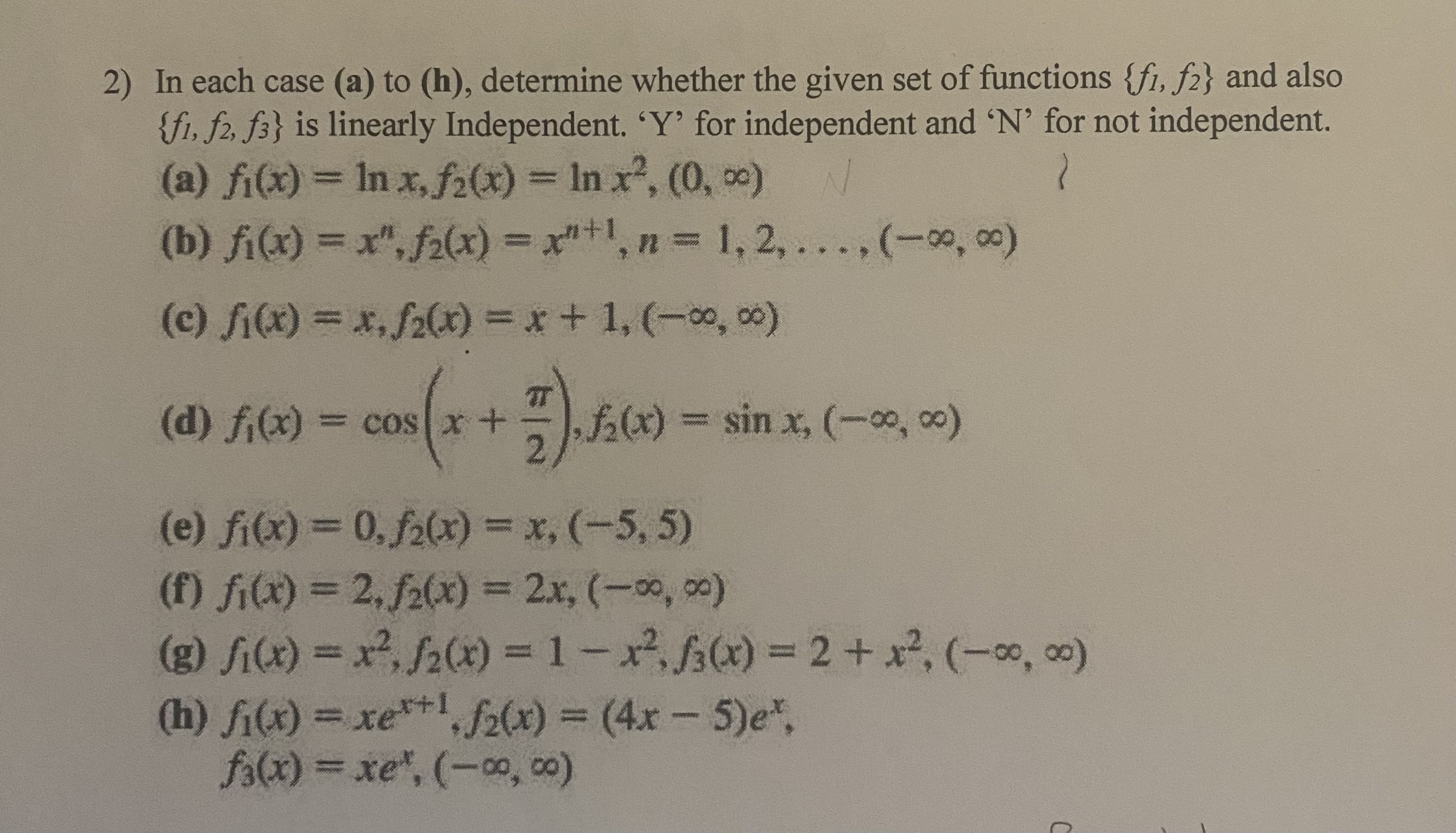Question: 2) In each case (a) to (h), determine whether the given set of functions {fi, f2} and also {f1, f2, f3} is linearly Independent. 'Y'

2) In each case (a) to (h), determine whether the given set of functions {fi, f2} and also {f1, f2, f3} is linearly Independent. 'Y' for independent and 'N' for not independent. (a) fi(x) = In x, f2(x) = In x-, (0, 09) (b) fi(x) = x", f2(x) = x+1, n = 1, 2, . ... (-09, 20) (e) fi(x) = x. f2(x) = x+ 1. (-00, 00) (d) fi(x) = cos x + " . f(x) = sin x, (-00, 00) (e) fi(x) = 0, f2(x) = x, (-5, 5) (f) fi(x) = 2. f2(x) = 2x, (-00, 00) (8) fi(x) = x2, f2(x) = 1 - x2, f3(x) = 2+ x2. (-00, 00) (h) fi(x) = xett, f2(x) = (4x - 5 )ex. fa(x) = xe, (-00, 60)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

3 Systems of differential equations Example 7. Let V be the set of all vector-valued solutions x(t)= of the vector differential equation (2) x=Ax, V is a vector space under the usual Operations of...

Differential Q1:- Find the general solution of the given differential equations: y(4) - 2y" + y = 0. Q2:- Let the differential equation (1): x2y" - 6xy' + 12y = 0, x E(0,co). a) Verify that the...

can someone solve this Modern workstations typically have memory systems that incorporate two or three levels of caching. Explain why they are designed like this. [4 marks] In order to investigate...

3 Systems of differential equations In Sections 3.8-3.10 we will reduce the problern of finding all solutions of (1) to the much simpler algebraic problern of solving simultaneous linear equations of...

Please help with the following questions!! Thank you in advance Lesson 6.1: Graphs of Relations Workbook 6A Lesson 6.1: Graphs of Relations Explore Your Understanding Assignment 1. The graph shows...

LAB 3: FUNCTIONS OF SEVERAL VARIABLES, PART B (c)2017 UM Math Dept licensed under a Creative Commons By-NC-SA 4.0 International License. 1. Objectives and Expectations for Lab 2, Part B Part B of Lab...

1. Determine if the following statements are TRUE or FALSE. Give reasons for your answers in each case. (a) The union of two subspaces of a vector space V is a subspace of V. (b) The intersection of...

dould you pls go through the answers step by step with the solutions attached and give some explanation and expanded working out method pls. Question 5. (a) We clearly have Lin(fo, fi, f2) = If If(x)...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

A water pipe bursts, flooding a Metal Fabrication Company utility room and tripping the circuit breakers on a panel in the room. Metal Fabrication contacts Nouri, a licensed electrician with five...

A drug manufacturer is considering how many of four new drugs to develop. Suppose it takes one year and $10 million to develop a new drug, with the entire cost being paid up front (immediately). The...

Please help with CapSim homework email: A . $ 1 3 7 , 7 7 1 B . $ 1 4 7 , 4 9 6 C . $ 1 3 1 , 2 8 8 D . $ 1 4 9 , 1 1 7

Evaluate the following loss estimation measures indicating the context from Mica Hardware in which each of them is applicable: 2.1. The maximum probable loss 2.2. The estimated maximum loss 2.3. The...