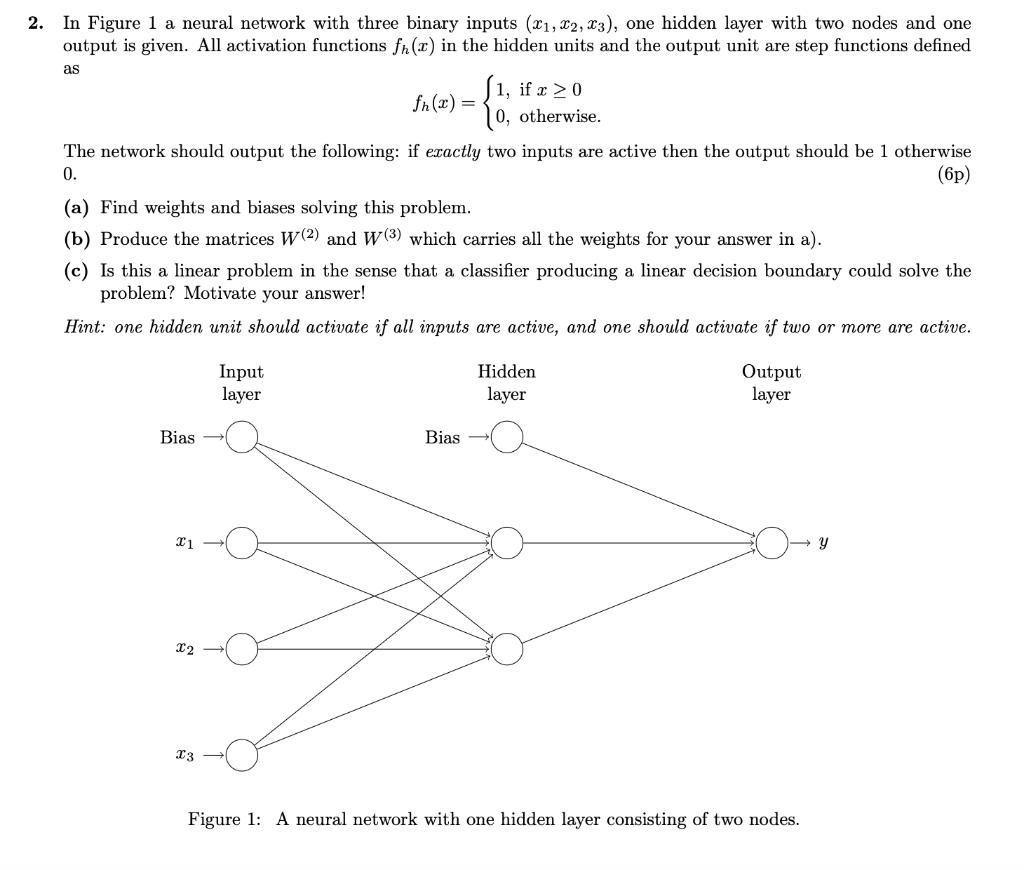
2. In Figure 1 a neural network with three binary inputs (x1, x2, x3), one hidden layer with two nodes and one output is given. All activation functions f(x) in the hidden units and the output unit are step functions defined as fn(2)= {1 1, if x 0 otherwise. The network should output the following: if exactly two inputs are active then the output should be 1 otherwise 0. (a) Find weights and biases solving this problem. (b) Produce the matrices W(2) and W (3) which carries all the weights for your answer in a). (6p) (c) Is this a linear problem in the sense that a classifier producing a linear decision boundary could solve the problem? Motivate your answer! Hint: one hidden unit should activate if all inputs are active, and one should activate if two or more are active. Input layer Bias x1 X2 23 Hidden layer Bias Output layer Figure 1: A neural network with one hidden layer consisting of two nodes. Y