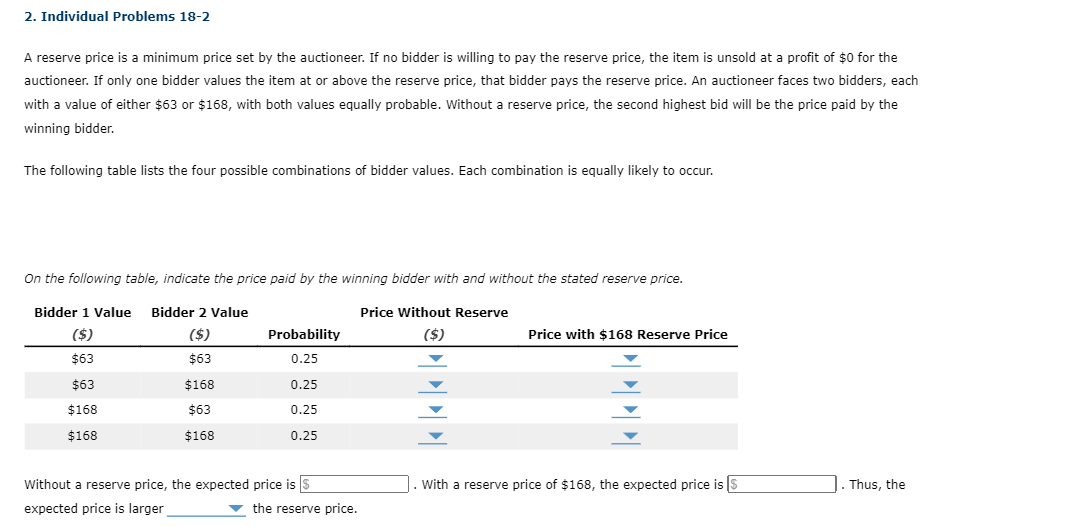
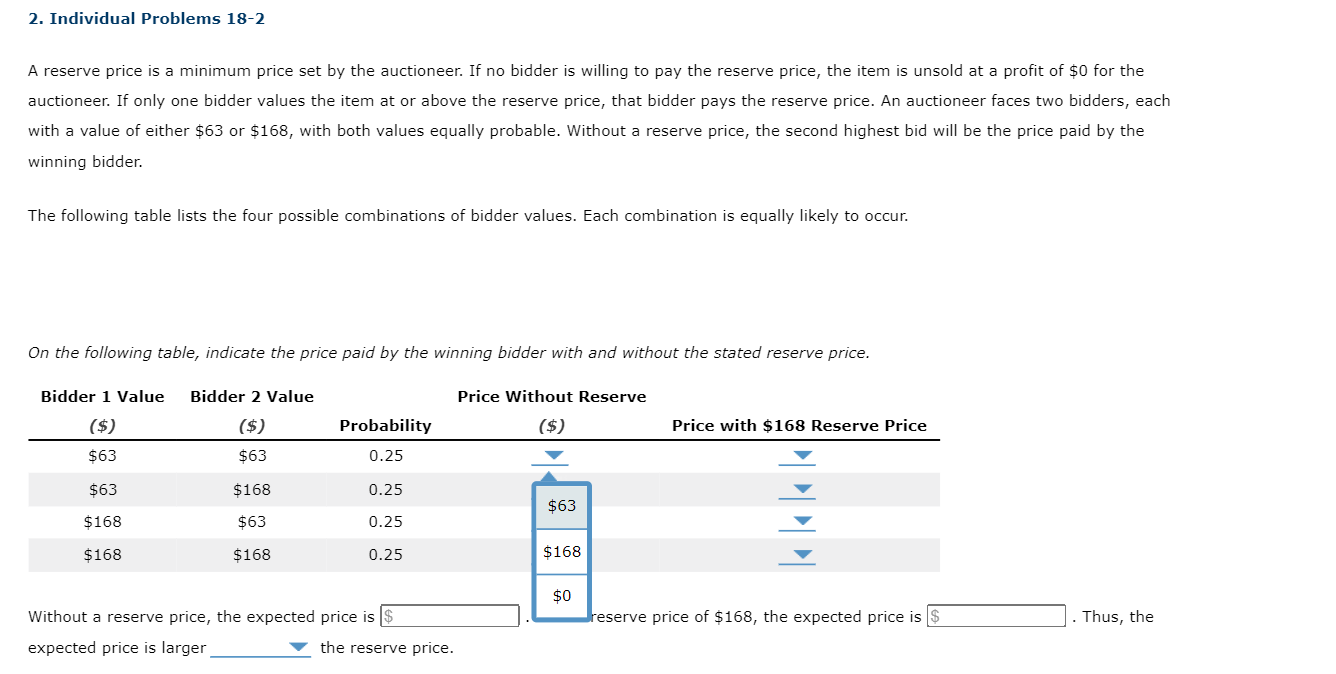
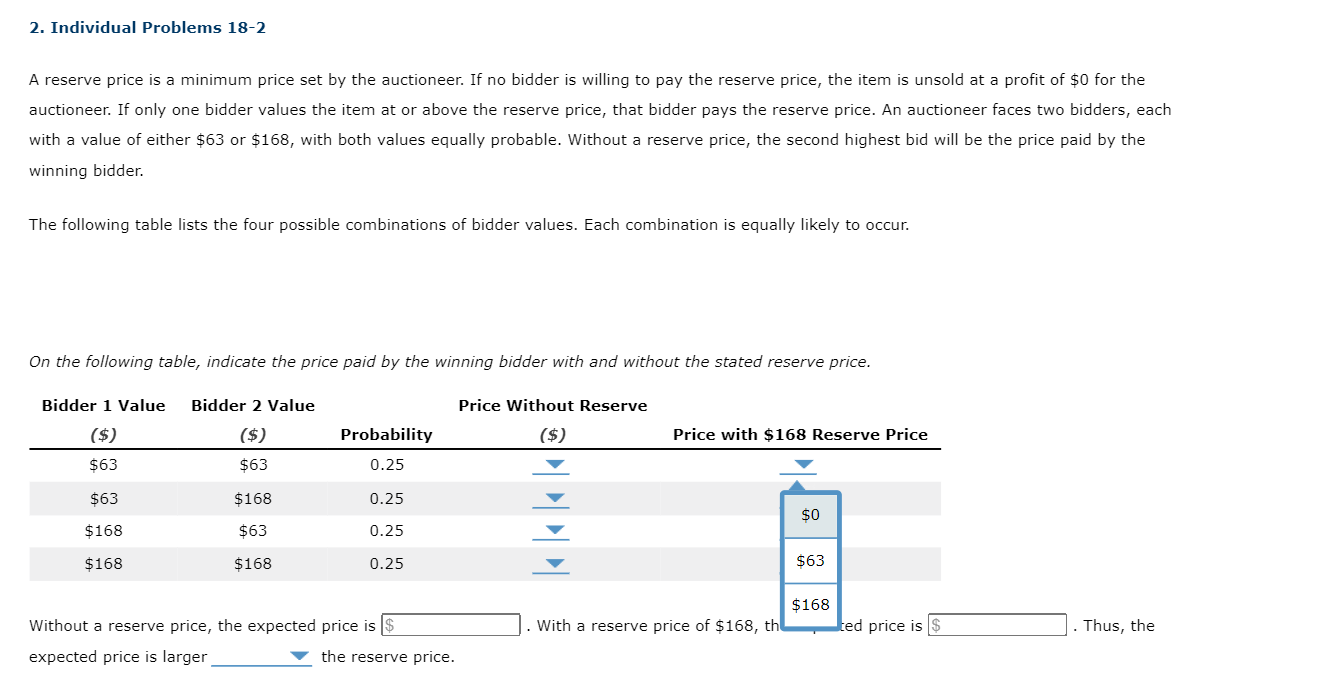
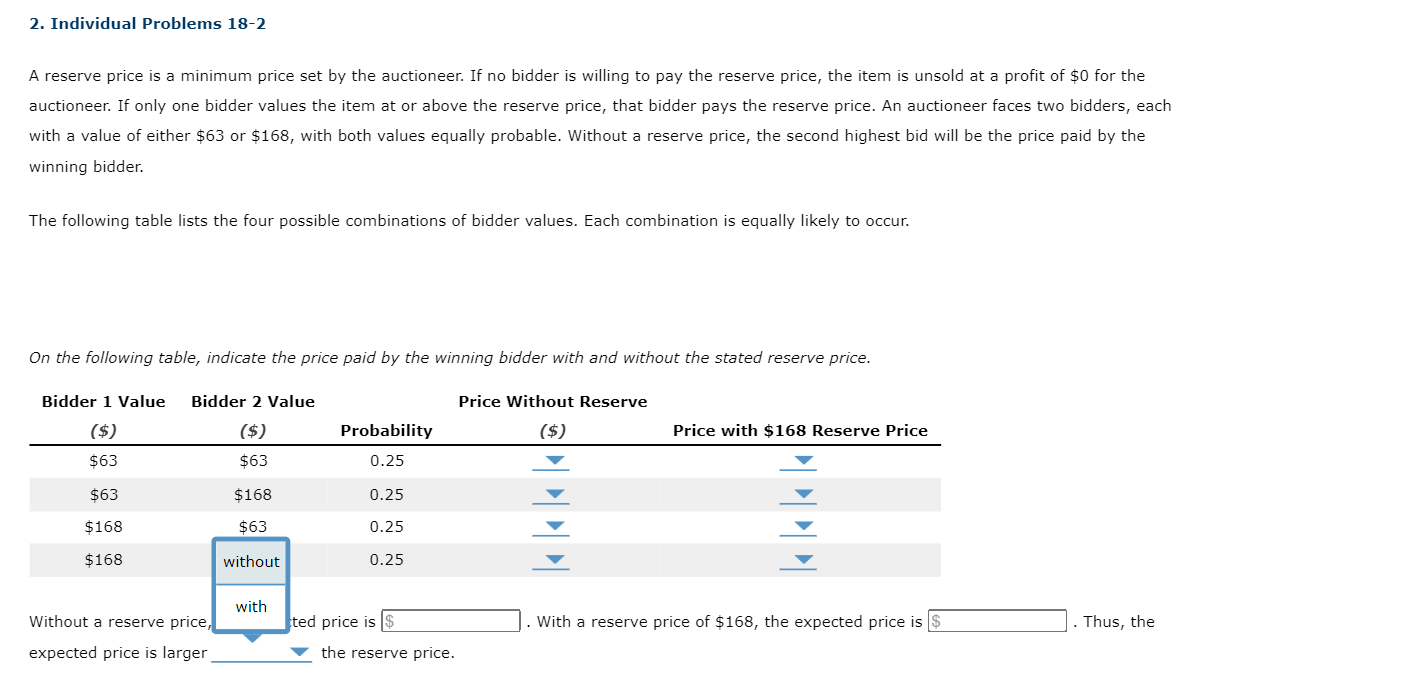
2. Individual Problems 18-2 A reserve price is a minimum price set by the auctioneer. If no bidder is willing to pay the reserve price, the item is unsold at a prot of $0 for the auctioneer. If only one bidder values the item at or above the reserve price, that bidder pays the reserve price. An auctioneer faces two bidders, each With a value of either $63 or $168, with both values equally probable. Without a reserve price, the second highest bid will be the price paid by the winning bidder. The following table lists the four possible combinations of bidder values. Each combination is equally likely to occur. On the following table, indicate the pn'ce paid by the winning bidder with and without the stated reserve price. Bidder 1 Value Bidder 2 Value Price Without Reserve {$) {$) Probability ($) Price with $168 Reserve Price $53 $63 p.25 ; _v $53 $168 0.25 l _" $168 $63 0.25 _v _v $168 $168 0.25 _V _'V Iu'u'ithout a reserve price, the expected price is . 1lllith a reserve price of $168, the expected price is _ .Thus, the expected price is larger V the reserve price. 2. Individual Problems 18-2 A reserve price is a minimum price set by the auctioneer. If no bidder is willing to pay the reserve price, the item is unsold at a prot of $0 for the auctioneer: If only one bidder values the item at or above the reserve price, that bidder pays the reserve price. An auctioneer i'aces two bidders, each With a value of either $63 or 5168, with both values equally probable. Without a reserve price, the second highest bid Will be the price paid by the Winning bidder. The following table lists the four p055ible combinations of bidder values. Each combination is equally likely to occur. On the followmg table, indicate the price paid by the Winning bidder with and without the stated reserve price. Bidder 1 Value Bidder 2 Value Price Without Reserve (5) (37) Probability (5) Price with $168 Reserve Price 563 $63 0.25 V 7 $63 $158 0.25 V $63 $168 $63 0.25 V $168 $168 0.25 $168 v $0 in .Thus, the Without a reserve price, the expected price is . eserve price of 5168, the expected price is expected price is larger V the reserve price. 2. Individual Problems 18-2 A reserve price is a minimum price set by the auctioneer. If no bidder is willing to pay the reserve price, the item is unsold at a profit of $0 for the auctioneer: If only one bidder values the item at or above the reserve price, that bidder pays the reserve price. An auctioneer faces two bidders, each with a value of either $63 or 5168, with both values equally probable. Without a reserve price, the second highest bid will be the price paid by the winning bidder. The following table lists the four possible combinations of bidder values. Each combination is equally likely to occur. On the following table, indicate the price paid by the winning bidder with and without the stated reserve price. Bidder 1 Value Bidder 2 Value Price Without Reserve (5) (5) Probability {5) Price with $168 Reserve Price 563 $63 0.25 V V $63 $168 0.25 7 $0 $168 $63 0.25 V $168 $168 0.25 V 563 $168 Without a reserve price, the expected price is . With a reserve price of 5168, th ed price is . Thus, the expected price is larger V the reserve price. 2. Individual Problems 18-2 A reserve price is a minimum price set by the auctioneer. If no bidder is willing to pay the reserve price, the item is unsold at a profit of $0 for the auctioneer: If only one bidder values the item at or above the reserve price, that bidder pays the reserve price. An auctioneer faces two bidders, each with a value of either $63 or 5168, with both values equally probable. Without a reserve price, the second highest bid will be the price paid by the Winning bidder. The followmg table lists the four p055ible combinations of bidder values. Each combination is equally likely to occur. On the foHowing table, indicate the price paid by the winning bidder with and without the stated reserve price. Bidder 1 Value Bidder 2 Value Price Without Reserve (5) (5?) Probability {33) Price with $168 Reserve Price 563 $53 0.25 l 7v $63 $168 0.25 L _v $168 $63 0.25 l 7" $168 0.25 l v ted price is . With a reserve price of 5168, the expected price is . Thus, the expected price is larger V the reserve price. Without a reserve price