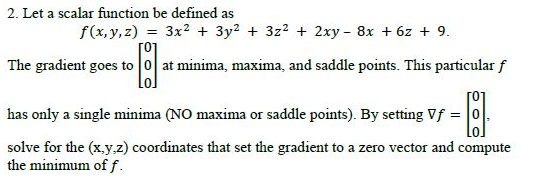
2. Let a scalar function be defined as f (x, y, z) = 3x2 + 3y' + 3z2 + 2xy - 8x + 6z + 9. The gradient goes to at minima, maxima, and saddle points. This particular f has only a single minima (NO maxima or saddle points). By setting Vf = solve for the (x,y,z) coordinates that set the gradient to a zero vector and compute the minimum of f