Question: 2. Let f : [0,1] > R be continuous and assume f(0) = f(1). Show that for each integer n > 1 there exists an

2. Let f : [0,1] > R be continuous and assume

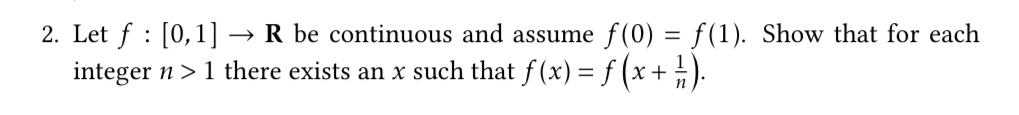
f(0) = f(1). Show that for each integer n > 1 there

2. Let f : [0,1] > R be continuous and assume f(0) = f(1). Show that for each integer n > 1 there exists an x such that f(x) : f (x + L). [I

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Q:

Solve the following: Let f : [0, 1] - R be continuous. Show that x 1 t x2 + . . . + an lim dx1 dx2 . . . dan = f n 2 lim f ((x122 . . . In) /) dx, dx2 . . . dan = f (?) n-too.Jo Jo

Q:

5. Let f : [0, 1] - R. be defined by TEQ f(I) = 1-1, 14Q (a) Show that f is injective on [0, 1). (b) Show that f(f ()) =T. (c) Where is f continuous on [0, 1]

Q:

nx (a) Let f (0, 1) R be given by fn(x) = +1. Show that {f} converges pointwise to a continuous function f, but the convergence is not uniform. (Remark: This shows that pointwise convergence to a...

Q:

Apply Epsilon Delta Definition Of A Limit or Squeeze Theorem to solve. (Intro to Real Analysis Bartle & Sherbert). Do not use L'Hpital's Rule. Note that x ?A = (0, inf) (question 1a) and x ? (-inf,...

Q:

(i) Let f : (0, 1] - R be a continuous function such that f is Riemann integrable on [x, 1] for every x > 0. Assume that given any c > 0, there exists d > 0 such that IS fl 0+ (ii) Show that the...

Q:

3. Let f : [0, 1] - R be defined as f(x) = r = 1 for any n E N, sin(x), x / 1. (a) Show that for any e > 0, there exists a continuous function g defined on 0, 1] such that If(x) - g(x) dx 0, there...

Q:

5. If E and F are connected subsets of M with E n F * O, show that E U F is connected. 8. If E and F are nonempty subsets of M, and if E U F is connected, show that EnFO. Throughout, M denotes an...

Q:

7.3 Some ancillary results 6. Weierstrass's approximation theorem. Let f : [0, 1] - R be a continuous function, and let Sn be a random variable having the binomial distribution with parameters n and...

Q:

Let f : [0, 1] } R be continuous and assume that f\" : (0, 1) > R is bounded on (0, 1). Suppose that the eeeent line from (U, f (0)) to (1, f (1)) intersects the graph of f at (1/\\/,f(1/\\/))- Show...

Q:

3. (a) Suppose f : [0, 1] - R is continuous and f(r) 2 0 on [0, 1]. If there exists ro E [0, 1] such that f(ro) > 0 then prove that fo f(x)dx > 0. (b) Let f(x) be continuous on [0, 1] and...

Q:

The budget director of Regal Furniture Company requests estimates of sales, production and other operating data from the various administrative units every month. Selected information concerning...

Q:

Use the following information to answer questions 2016 $6,000 $44,000 $600 $18,000 Prepaid rent Amount paid for rent Utilities payable Amount paid for utilities 4 How much was rent expense during...

Q:

What are the attributes of the majority of customers purchasing the product of your company (e.g., early adopters, early majority, late majority)? What does this tell you about the strategic issues...

Q:

1, You calculate that your time between orders for can labels in a periodic review inventory should be set at 20 days. Your lead time for this item is 5 days and your supplier has shown no variation...

Q:

An improvement in the exchange of information in negotiations.

Q:

1. Effort is important.

Q:

2. Set up two points representing the pillars of your values system. Discuss this with the others in the group.