Question: 2. Let G be a group and a, b, E G. (a) Prove that (ab)-1 = b-la-1. (b) Prove that (a ])-1 = a. (c)
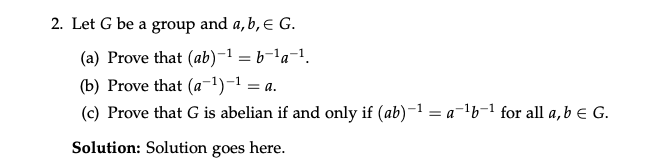
![(a) Prove that (ab)-1 = b-la-1. (b) Prove that (a ])-1 =](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6703ef7096711_1526703ef707302d.jpg)



2. Let G be a group and a, b, E G. (a) Prove that (ab)-1 = b-la-1. (b) Prove that (a ])-1 = a. (c) Prove that G is abelian if and only if (ab) -1 = a b- for all a, be G. Solution: Solution goes here.Solution : Given to be a group Now also a, b EG. Now wing the properties of the quoup we have to prove, win the given parts. Co ) in we have to prove (abjt = bta-! Now Since Got in a group therefore ( ab) + EG.. we have wed closure property (if a, b EG =) ab EG) and existence of inverve, since ( ab) EG there fore ( ab - 1 ) EG. Now if be in a group that there exists an identity element, let e bethat element if at G then there exist eEG's ae = a = ea thing the property ofthe identity element we have , (ab ) ( ab)= =e Now operating both eider by and a - 1 ( ab ) ( ab- 3 ) = ate ( a-za ) ( b ) ( ab- + ) = and (: a (bc) = (ab) (, # a,bic ( on )eb ( ab ) = a - 1 b ( ab- 4 ) = a - 1 Now by b - 1 b - b ( ab ) - 1 = 6-ta - 1 e ( ab ) - = bla - 1 ( ab) 1 = b-la- 1 juce the proof of part (a). by we have to prove that ( at ) 1 = a Now ming the invove property of Group, we know if GEG satEma( at EG. Then we can write. ( a-+ ) ( at]-) = e Operating both aide boy a (at ) ( a-t ) - = ac ( aat ) ( at ) - 1 = a eca- 1 7 - a ( at ) ] = a Proof of part (b).CJ As we have in the first part that a ,b E G (ab ) 2 = bla+ Now it in given that Ge is an abelian group, therefore we have Va, bEG =) ab= ba Now from the property of existance of inverse . if atme = Jat EG and if BEG EJ DOGG then we can write d Now cuting part ( a) ( ab) - 1 = 6-tat = atb-1 (ab ) = a- 1b- 1 Now convorely, Let ( ab)- 1= a-16 - 1 then we have to prove that or in abelian Let arbEG then abEG and cab-Is EG (ab ) (abj- ] = e ( ab)albaize Operating both side by b ( ab )a- bib = eb = b ( ab ) ate = b ( ab ) at = 6Now DJ a, ( ab ) ata = ba ( ab) e = ba ab = ba # a, bel which chow Ge is abelian group
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


