Question: 2. Let X be a random variable with continuous distribution function F(x;0), and you wish to test Ho : 0 = 0o. (a) (5 points)


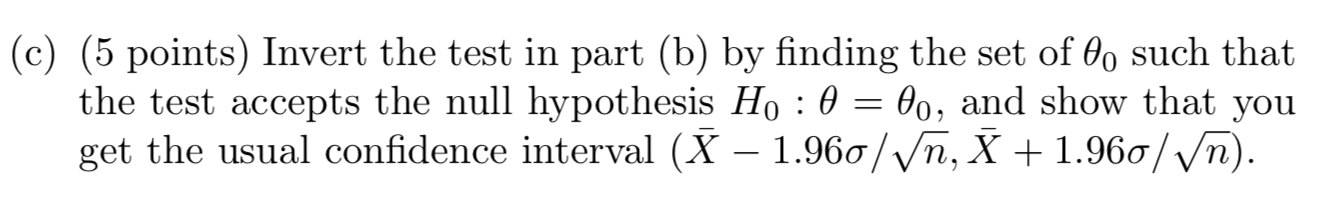
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


