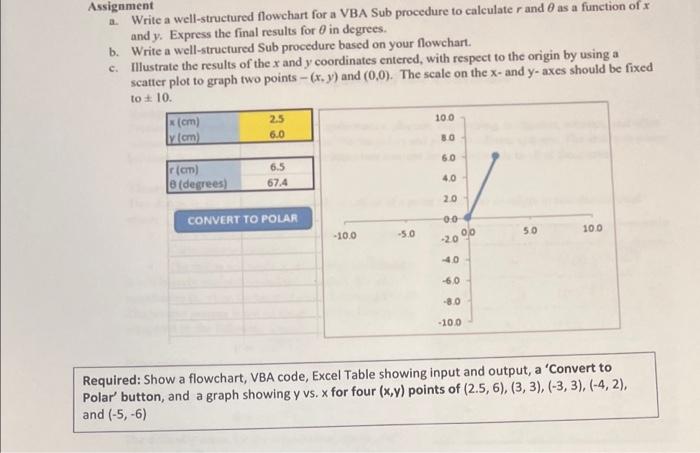
Question: 2) Polar Coordinate Conversion (12 Points) Technical Computation Rectangular to Polar Conversion Background Professionals working in the fields of mathematics, physies, engineering, navigation, robotics, and
2) Polar Coordinate Conversion (12 Points) Technical Computation Rectangular to Polar Conversion Background Professionals working in the fields of mathematics, physies, engineering, navigation, robotics, and other sciences, visualize data in both Cartesian (rectangular) and polar coordinate systems. The ability to move between these coordinate systems is an important concept for professionals in all of these areas. Theory Two distances are required to specify the location of a point relative to an origin in two dimensional space: - The horizontal and vertical distances (x,y) in Cartesian coordinates, or - The radius and angle (r,) in polar coordinates It is relatively straightforward to compute Cartesian coordinates (x,y) on the basis of polar coordinates (r,). The reverse process is not so simple. The radius can be computed by the following formula: r=x2+y2 If the coordinates lie in the first or fourth quadrant (i.e., x>0 ), then the following simple formula can be used to compute : =tan1(xy) The difficulty arises for the other two quadrants and when x=0. The table summarizes the possibilities. Assignment a. Write a well-structured flowchart for a VBA Sub procedure to calculate r and as a function of x and y. Express the final results for in degrees. b. Write a well-structured Sub procedure based on your flowchart. c. Illustrate the results of the x and y coordinates entered, with respect to the origin by using a scatter plot to graph two points (x,y) and (0,0). The scale on the x - and y-axes should be fixed to 10. Required: Show a flowchart, VBA code, Excel Table showing input and output, a 'Convert to Polar' button, and a graph showing y vs. x for four (x,y) points of (2.5,6),(3,3),(3,3),(4,2), and (5,6) 2) Polar Coordinate Conversion (12 Points) Technical Computation Rectangular to Polar Conversion Background Professionals working in the fields of mathematics, physies, engineering, navigation, robotics, and other sciences, visualize data in both Cartesian (rectangular) and polar coordinate systems. The ability to move between these coordinate systems is an important concept for professionals in all of these areas. Theory Two distances are required to specify the location of a point relative to an origin in two dimensional space: - The horizontal and vertical distances (x,y) in Cartesian coordinates, or - The radius and angle (r,) in polar coordinates It is relatively straightforward to compute Cartesian coordinates (x,y) on the basis of polar coordinates (r,). The reverse process is not so simple. The radius can be computed by the following formula: r=x2+y2 If the coordinates lie in the first or fourth quadrant (i.e., x>0 ), then the following simple formula can be used to compute : =tan1(xy) The difficulty arises for the other two quadrants and when x=0. The table summarizes the possibilities. Assignment a. Write a well-structured flowchart for a VBA Sub procedure to calculate r and as a function of x and y. Express the final results for in degrees. b. Write a well-structured Sub procedure based on your flowchart. c. Illustrate the results of the x and y coordinates entered, with respect to the origin by using a scatter plot to graph two points (x,y) and (0,0). The scale on the x - and y-axes should be fixed to 10. Required: Show a flowchart, VBA code, Excel Table showing input and output, a 'Convert to Polar' button, and a graph showing y vs. x for four (x,y) points of (2.5,6),(3,3),(3,3),(4,2), and (5,6)