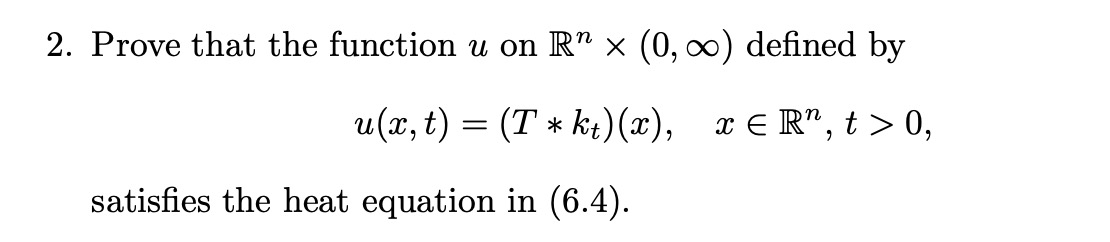
2. Prove that the function u on R" x (0, co) defined by u(xx, t) = (T * kt) (2), x ER", t> 0, satisfies the heat equation in (6.4).Theorem 6.4 Let f E LP(R"), 1 0. Then Ilu( ., t) 1/p 0. Proof Obviously, for t > 0, | | kt * fll1 5 (47t) -"/21/fll1, f E L'(Rn). By Young's inequality in Theorem 3.2, we get for t > 0, | Kt * flloo 0. 0 Theorem 6.4 is an LP-LP estimate. If we use the Riesz-Thorin theorem differently, then we can get an LP-LP estimate