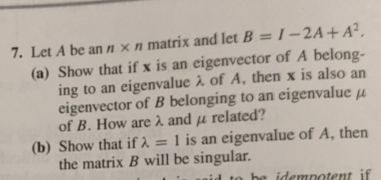
2. Show that the eigenvalues of a triangular matrix are the diagonal elements of the matrix. 3. Let A be an n x / matrix. Prove that A is singular if and only if ) = 0 is an eigenvalue of A. 4. Let A be a nonsingular matrix and let ) be an eigen- value of A. Show that 1/2. is an eigenvalue of A-.7. Let A be an n x n matrix and let B = /-2A + A?. (a) Show that if x is an eigenvector of A belong- ing to an eigenvalue 1 of A, then x is also an eigenvector of B belonging to an eigenvalue / of B. How are A and u related? (b) Show that if A = 1 is an eigenvalue of A, then the matrix B will be singular. idempotent if