Question: 2. Suppose that f : t > R is continuous at C, and that f((:) > k for some real number k. Prove that there

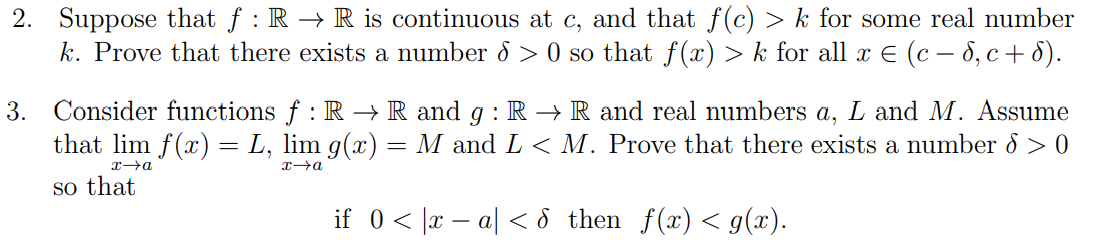
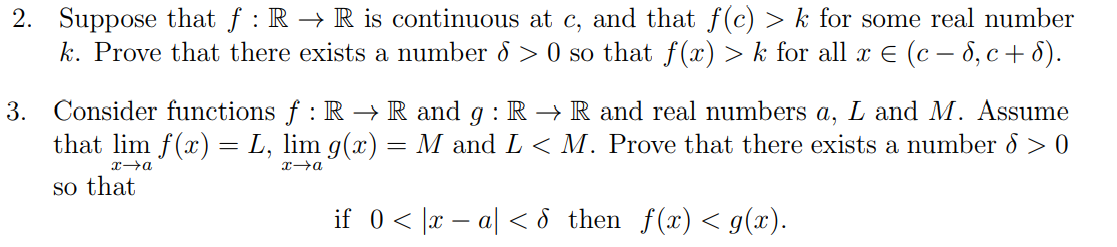
2. Suppose that f : t > R is continuous at

2. Suppose that f : t > R is continuous at C, and that f((:) > k for some real number k. Prove that there exists a number (5 > 0 so that f(:1:) > k for all :1: E (c (31 c + 5). 3. Consider functions f : R > R and g : R > R and real numbers a, L and 11:1. Assume that lim f(:1:) = L, lim 9(33) 2 M' and L 0 935'1'1 xra so that if 0

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Could someone please check my work Please state all definitions and theorems that you Will need: Definition 5.2.1 L9t f3 D E and let 4* ., D. We say that [is continuous at r' if A. l ' 6 nd i _ . r...

I know this proof is correct but could someone please answer my questions in black ink for all x E R . A function f: R - R is said to be periodic if there exists a number k > 0 such that f(a + k) =...

Could someone please check my work Please state all definitions and theorems that you will need: Thearea 5.4He Suppose of: D ->Ro is continuous on a compact set is . Then of is uniformly continuous...

Suppose that f : R -> R is continuous on all of R. What is the maximum number of distinct vertical asymptotes that f can have? (a) 0 (b) 1 (c) 2 (d) Infinitely many Which of the following is equal to...

(a) Let ACS CR, and c A be a point. Suppose f: S R is continuous at c. Prove that the restriction f| is continuous at c. (b) Find an example of a function f : S R and a subset AC S such that | is...

Could someone please check my work Theorem 5.2.10 Let f and g be functions from D to R , and let c E D . Suppose that f and g are continuous at c. Then (a) f + g and fg are continuous at c , and (b)...

Could someone please help me with this problem A function f: R - R is said to be periodic if there exists a number k > 0 such that f(a + k) = f(a) for all a E R. Suppose that f : R - R is continuous...

Could someone please help me with this problem A function f : R - R is said to be periodic if there exists a number k > 0 such that f(a + k) = f(x) for all E R . Suppose that f : RR - R is continuous...

(a) Prove that if] Q I and f : I > R is continuous at C E I, then f | I is continuous at C. (b) Give a function f : R > R such that the following holds, where I = [0, 1]. There is a C E I such that f...

Show that n! can be represented as the sum of n of its distinct positive divisors whenever n 3.

All false. Reconsider the previous exercise. Now suppose that the p-value from the ANOVA F-test turns out to be 0.003. All of the following statements are false. Explain why each one is false. a. The...

Suppose that f ( x ) = 1 x , x 0 , and g ( x ) = x 2 , x 0 . ( a ) Find ( f @ g ) ( x ) together with its domain. ( b ) Find ( g @ f ) ( x ) together with its domain.

Consider a pendulum, of length l and a bob of mass mat its end, moving through a lubricated oil with decreasing 0. The massive bob undergoes small oscillations, but the oil retards the bob's motion...

find the D( mechanical energy, E frequency of the damped motion, F quality factor. Consider a pendulum, of length l and a bob of mass mat its end, moving through a lubricated oil with decreasing 0....

2. Solve explicitly ur,e + Uy,y 0 on Ba(0) C R with the boundary condition u(a cos 0, a sin 0) = (a, 0) = 1+ 3 sin 0. Write your solution in Euclidean coordinates. Hint: Apply the Poisson for- ula.

1. A gas at 52.2 psi gauge pressure occupies 32.1 ft. Find the volume of the gas when the pressure is decreased to 77.5 psi. (Assume the temperature is held constant.)

Tanger Company purchased a delivery truck for R$38,000 on January 1, 2017. The truck has an expected residual value of R$6,000, and is expected to be driven 100,000 miles over its estimated useful...

The Robotics Manufacturing Company operates an equipment repair business where emergency jobs arrive randomly at the rate of two jobs per 8 -hour day. The company's repair facility is a single-server...

9. How much of the information collected will be used in decision-making?

1. Background knowledge of the subject and

4. What specific changes in the environment have taken place in relation to the information we have collected?