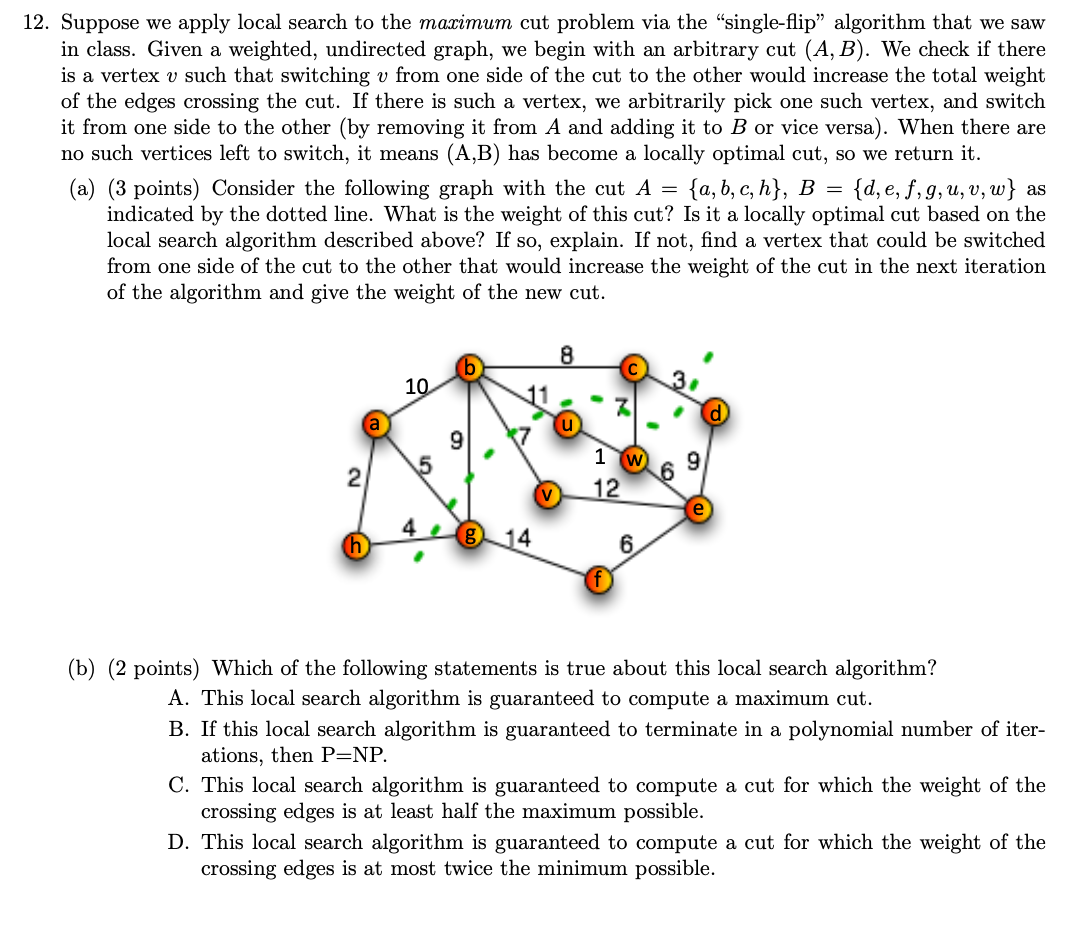
2. Suppose we apply local search to the maximum cut problem via the "single-flip" algorithm that we saw in class. Given a weighted, undirected graph, we begin with an arbitrary cut (A,B). We check if there is a vertex v such that switching v from one side of the cut to the other would increase the total weight of the edges crossing the cut. If there is such a vertex, we arbitrarily pick one such vertex, and switch it from one side to the other (by removing it from A and adding it to B or vice versa). When there are no such vertices left to switch, it means (A,B) has become a locally optimal cut, so we return it. (a) (3 points) Consider the following graph with the cut A={a,b,c,h},B={d,e,f,g,u,v,w} as indicated by the dotted line. What is the weight of this cut? Is it a locally optimal cut based on the local search algorithm described above? If so, explain. If not, find a vertex that could be switched from one side of the cut to the other that would increase the weight of the cut in the next iteration of the algorithm and give the weight of the new cut. (b) (2 points) Which of the following statements is true about this local search algorithm? A. This local search algorithm is guaranteed to compute a maximum cut. B. If this local search algorithm is guaranteed to terminate in a polynomial number of iterations, then P=NP. C. This local search algorithm is guaranteed to compute a cut for which the weight of the crossing edges is at least half the maximum possible. D. This local search algorithm is guaranteed to compute a cut for which the weight of the crossing edges is at most twice the minimum possible