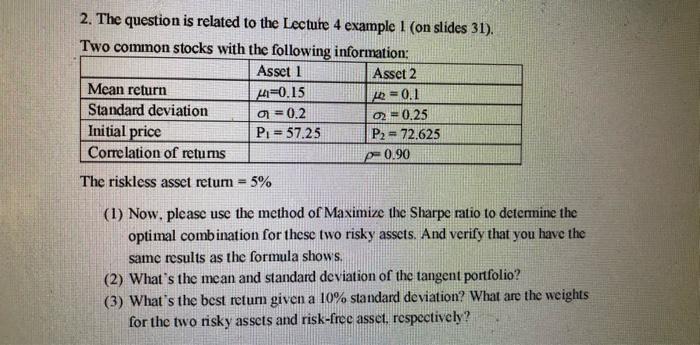
2. The question is related to the Lecture 4 example 1 (on slides 31). Two common stocks with the following information: Asset 1 Asset 2 Mean return 4-0.15 0.1 Standard deviation 0 =0.2 02 = 0.25 Initial price P1 = 57.25 P2 = 72.625 Correlation of retums pe 0.90 The riskless assct retum = 5% (1) Now, please use the method of Maximize the Sharpe ratio to determine the optimal combination for these two risky assets. And verify that you have the same results as the formula shows. (2) What's the mean and standard deviation of the tangent portfolio? (3) What's the best return given a 10% standard deviation? What are the weights for the two risky assets and risk-free asset. respectively? 2. The question is related to the Lecture 4 example 1 (on slides 31). Two common stocks with the following information: Asset 1 Asset 2 Mean return 4-0.15 0.1 Standard deviation 0 =0.2 02 = 0.25 Initial price P1 = 57.25 P2 = 72.625 Correlation of retums pe 0.90 The riskless assct retum = 5% (1) Now, please use the method of Maximize the Sharpe ratio to determine the optimal combination for these two risky assets. And verify that you have the same results as the formula shows. (2) What's the mean and standard deviation of the tangent portfolio? (3) What's the best return given a 10% standard deviation? What are the weights for the two risky assets and risk-free asset. respectively