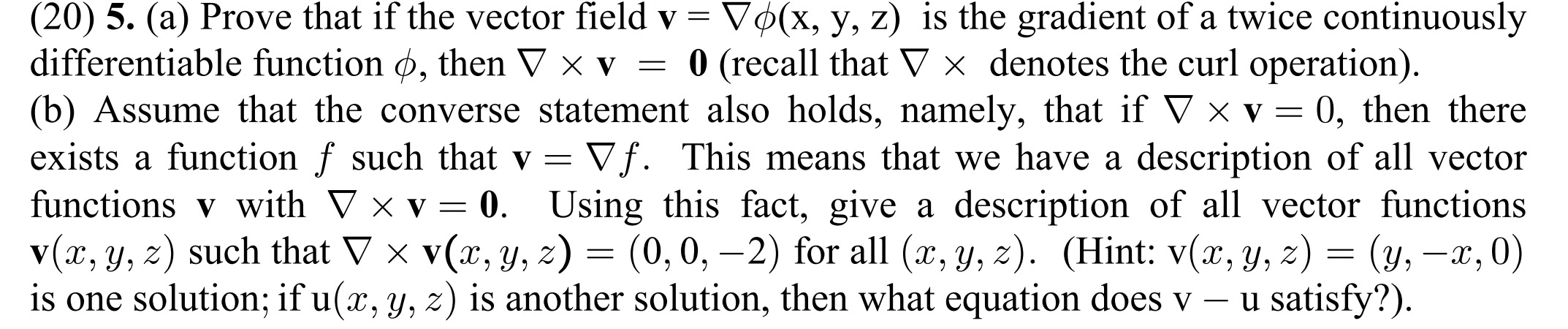
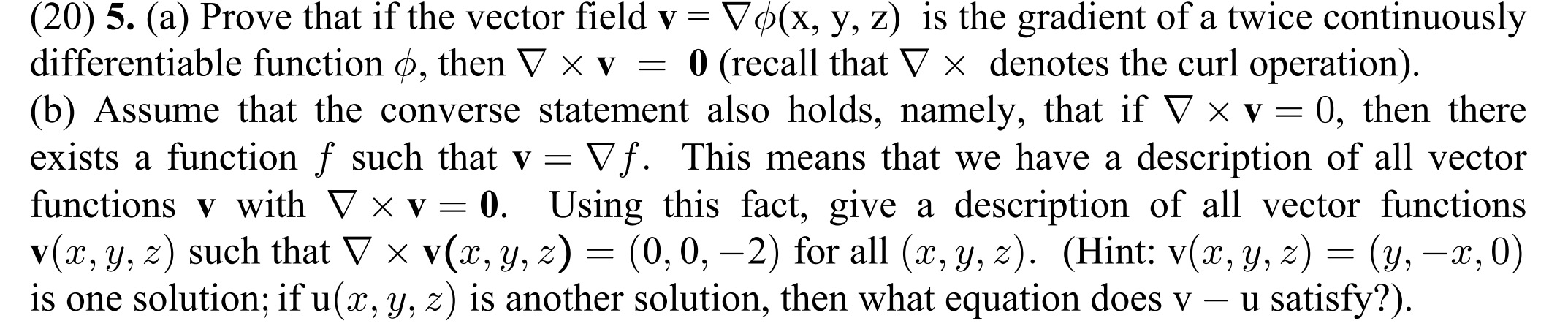
(20) 5. (a) Prove that if the vector eld V = Vq5(x, y, z) is the gradient of a twice continuously differentiable function gt), then V X V = 0 (recall that V X denotes the curl operation). (b) Assume that the converse statement also holds, namely, that if V X V = 0, then there exists a function f such that V = V f . This means that we have a description of all vector functions V with V X V = 0. Using this fact, give a description of all vector functions V(a:,y, 2) such that V x V(U,'y, z) = (0,0, 2) for all (m, y, z). (Hint: V(m,y, z) = (y,:1:,0) is one solution; if u(:c, y, z) is another solution, then What equation does V u satisfy?)