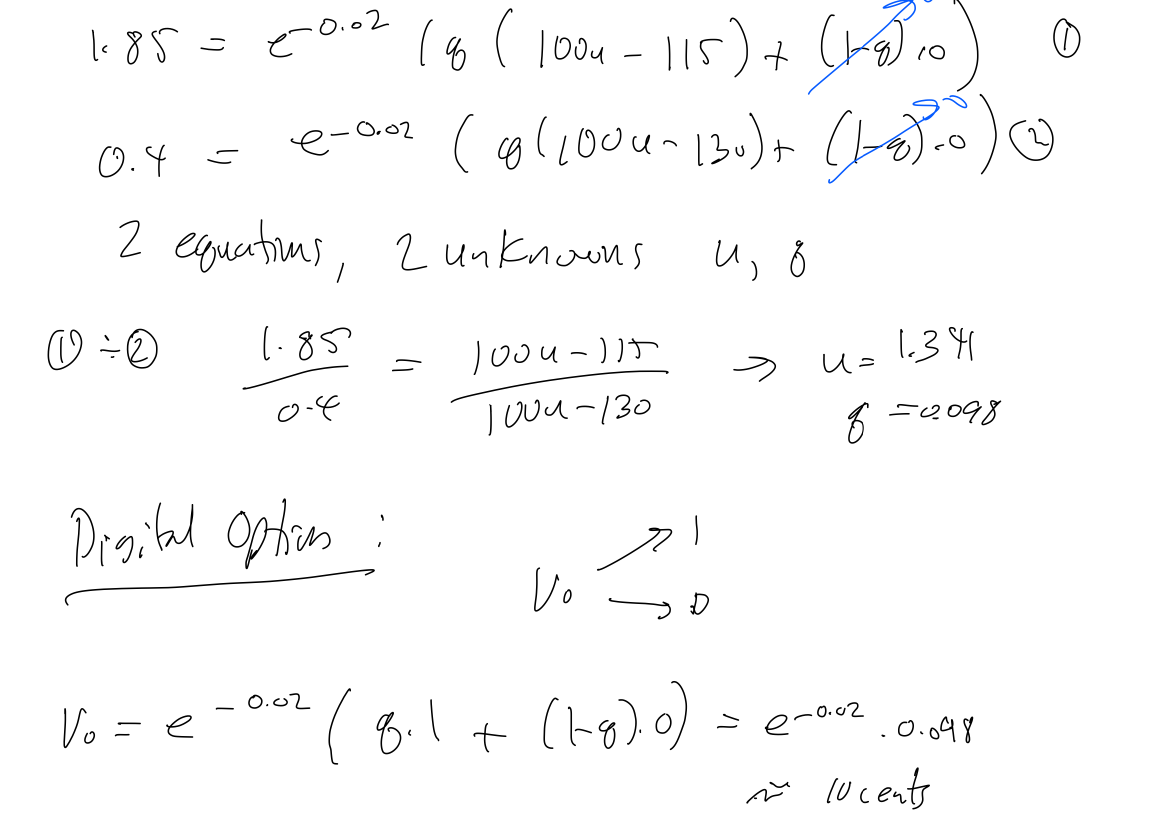
2.15 = 1.85

0.36 = 0.40

u = 1.330

g = 0.121

v0 = 12 cents

b) Calculate the drift of the stock in the above model if the probability that the stock price rises is p = 0.80.

The answer for a is 12 cents. I don't need (a), I need b.

5. (a) Suppose that a stock currently trades for $100, that the risk-free interest rate is 2% per annum, and European call options with expiry in 1 year have strike prices of $115 and $130, and currently trade for $2.15 and $0.36, respectively. Use a 1-period binomial tree to estimate the present value of a digital call option (on the same stock with the same expiry) with a strike price of $110. 7. Pmplied Volutility stock model Assume market prices are cossect. 1.85=e0.02(8(1004115)+(18)10)0.4=e0.02(8(100u130)+(18)80)(2) 2 equations, 2 unknowns u,8 (1) (2) 0.41.85=100u130100u115u=1.348=0.098 Pigital Option: V0=e0.02(81+(18)0)=e0.020.098 5. (a) Suppose that a stock currently trades for $100, that the risk-free interest rate is 2% per annum, and European call options with expiry in 1 year have strike prices of $115 and $130, and currently trade for $2.15 and $0.36, respectively. Use a 1-period binomial tree to estimate the present value of a digital call option (on the same stock with the same expiry) with a strike price of $110. 7. Pmplied Volutility stock model Assume market prices are cossect. 1.85=e0.02(8(1004115)+(18)10)0.4=e0.02(8(100u130)+(18)80)(2) 2 equations, 2 unknowns u,8 (1) (2) 0.41.85=100u130100u115u=1.348=0.098 Pigital Option: V0=e0.02(81+(18)0)=e0.020.098