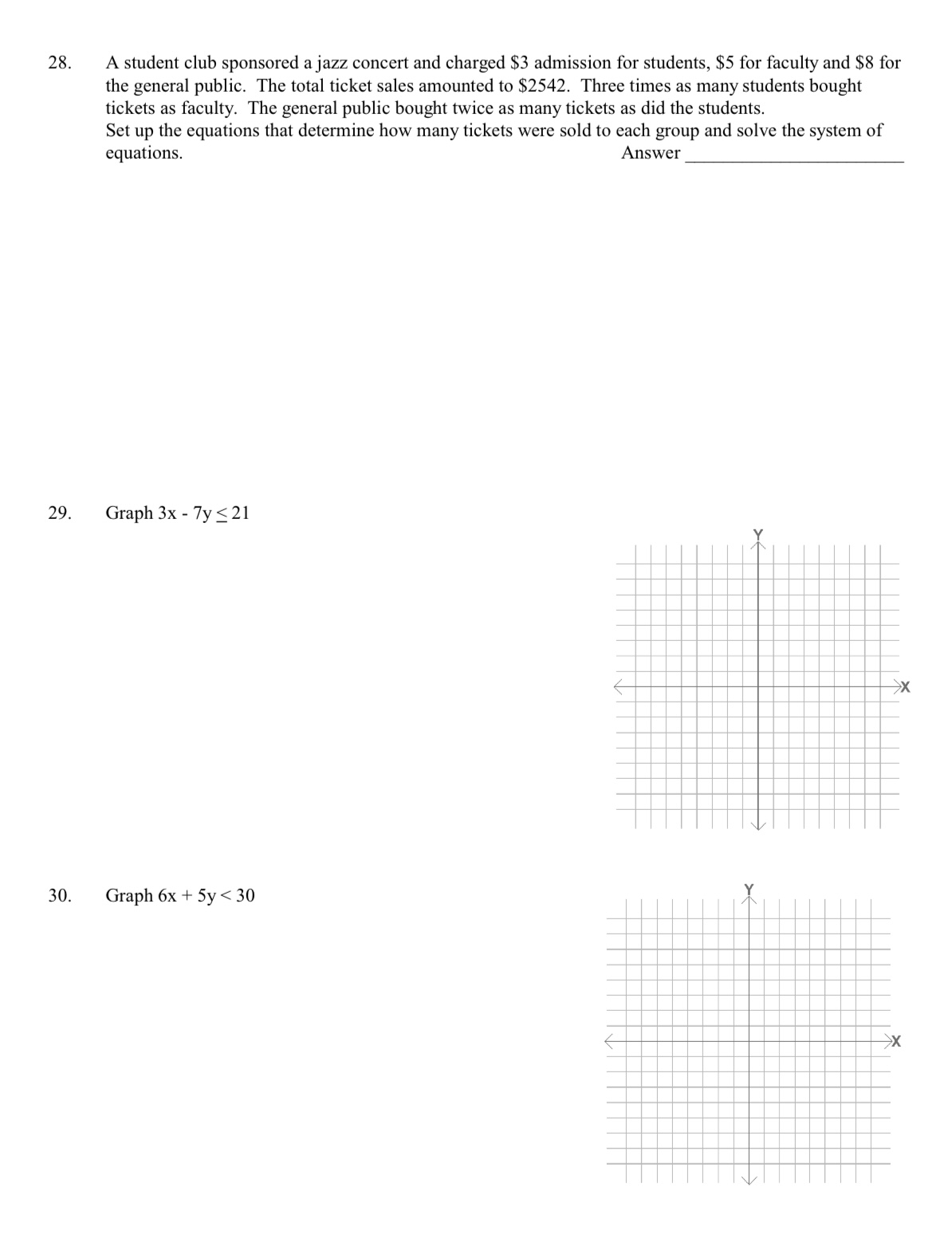
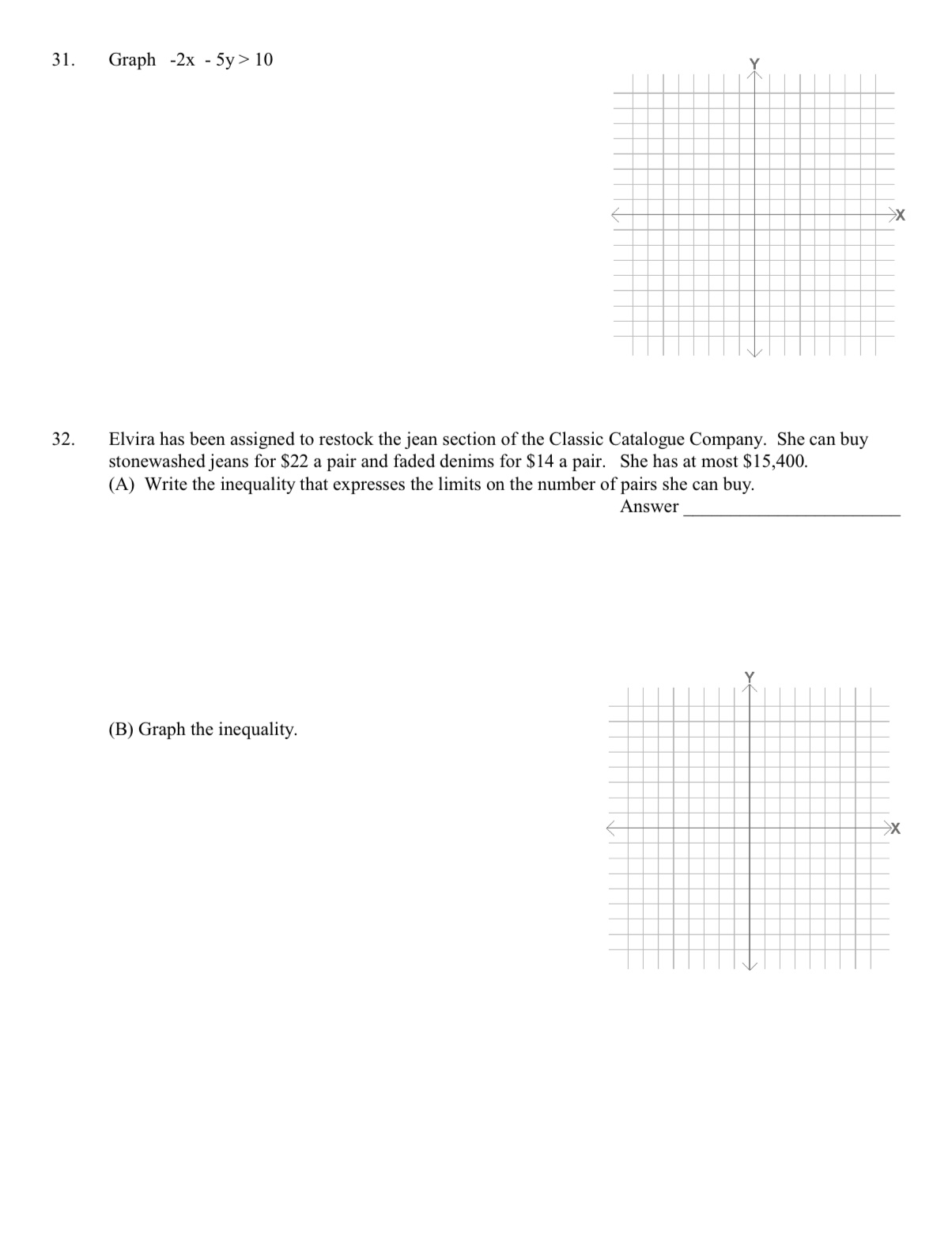
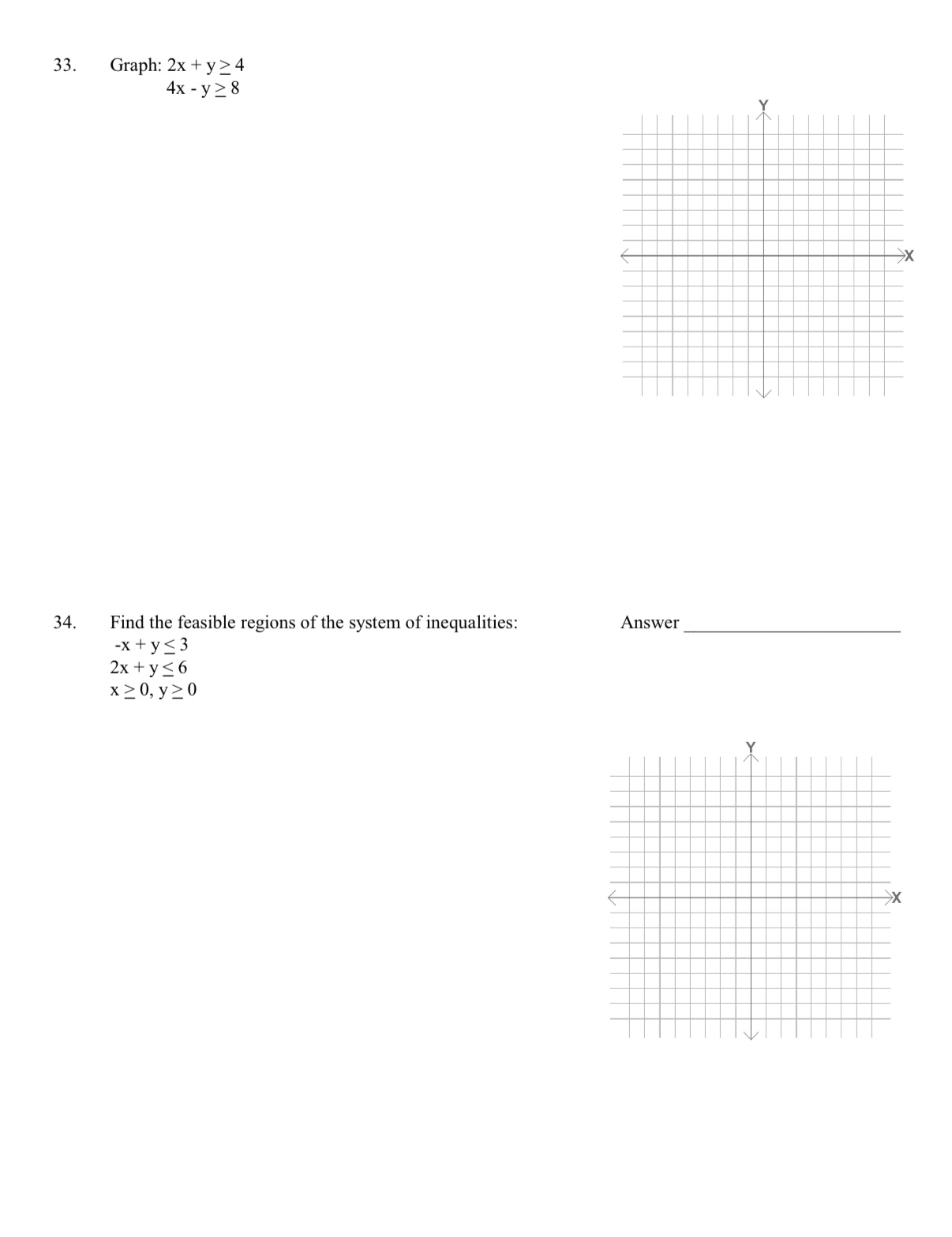
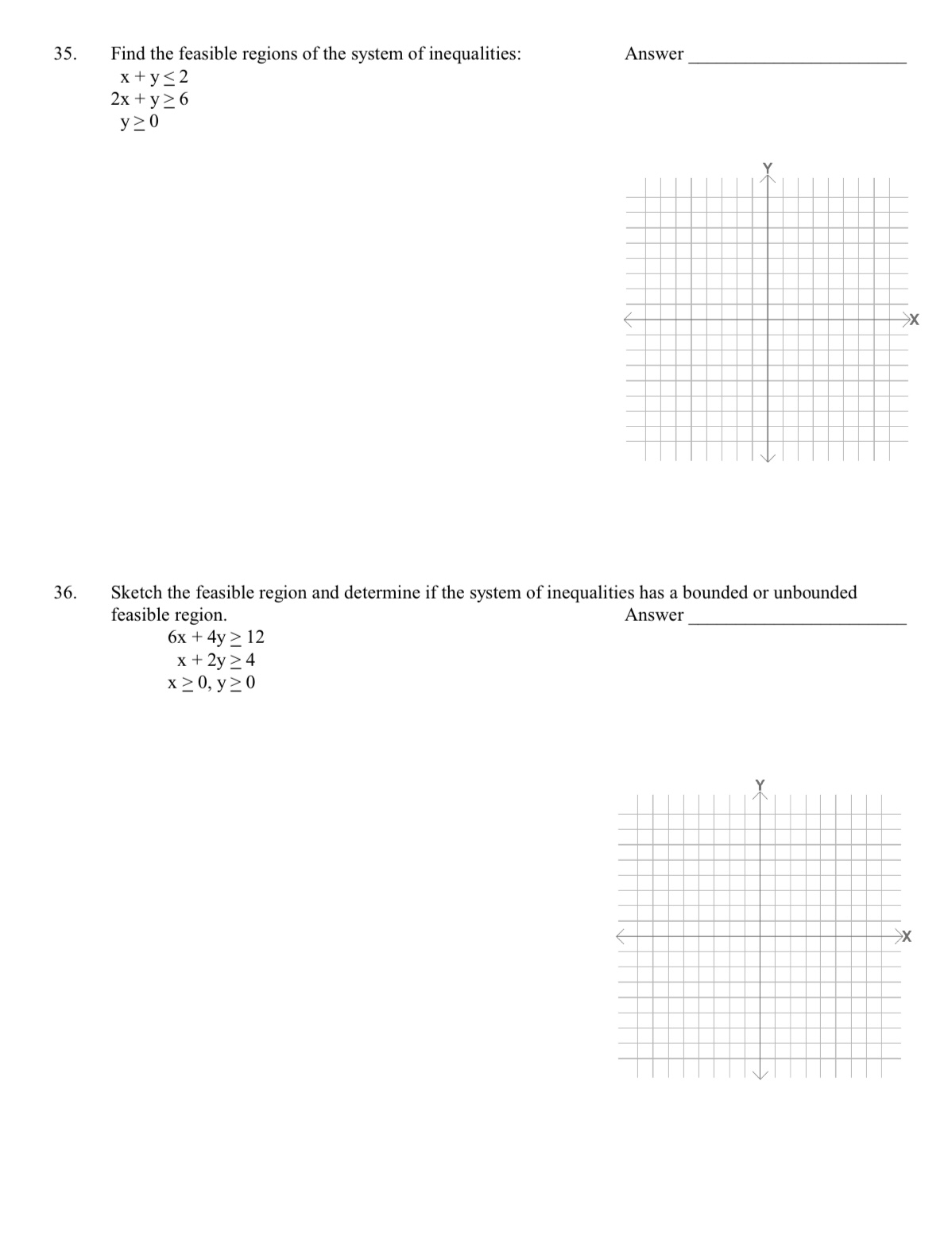
25. Determine the augmented matrix for: X+ x2 + x3 = 9 5x+3x2+6x = 21 X 4x2 + x3 = 7 26. Answer Write the system of equations represented by the augmented matix: Answer 1 4 -1 2 1 2 -35 1 2506 27. Solve using an augmented matrix: 2x + 3y = 5 x-2y=-1 Answer 28. A student club sponsored a jazz concert and charged $3 admission for students, $5 for faculty and $8 for the general public. The total ticket sales amounted to $2542. Three times as many students bought tickets as faculty. The general public bought twice as many tickets as did the students. Set up the equations that determine how many tickets were sold to each group and solve the system of equations. Answer 29. Graph 3x-7y 21 30. Graph 6x+5y < 30 >x >x 31. Graph -2x 5y > 10 - 32. Elvira has been assigned to restock the jean section of the Classic Catalogue Company. She can buy stonewashed jeans for $22 a pair and faded denims for $14 a pair. She has at most $15,400. (A) Write the inequality that expresses the limits on the number of pairs she can buy. (B) Graph the inequality. Answer >X 33. Graph: 2x + y 4 4x-y > 8 34. Find the feasible regions of the system of inequalities: Answer -x + y 3 2x + y 6 x0, y 0 x x 35. Find the feasible regions of the system of inequalities: x + y 2 Answer 36. 2x + y 6 y 0 Sketch the feasible region and determine if the system of inequalities has a bounded or unbounded Answer feasible region. 6x + 4y > 12 x + 2y 4 x 0, y 0 x 37. The Musical Group has two admission prices for its concerts, $12 for adults and $6 for students. They will not book a concert unless they are assured an audience of at least 500 people and total ticket sales of $5400 or more. Write the constraints on the number of each kind of ticket sold. Answer 38. Find the maximum and minimum value of z = 6x + 15y Answer X 39. Find the maximum value of the objective function z = 20x + 12y, subject to the constraints: Answer 3x + 2y 18 3x + y 15 40. x 0, y0 Minimize z 2x + 3y subject to: 4x + y 40 4x + 3y 64 x0, y 0 Answer x 41. Maximize z = 3x + y subject to: 2x-3y > 10 X > 8 x0, y 0 42. Answer The Nut Factory produces a mixture of peanuts and cashews. The company guarantees that at least 40% of the total weigh is cashews. It has a contract to produce 1000 pounds or more of the mixture. The peanuts cost $0,80 per pound, and the cashews cost $1.50 per pound. Find the amount of each kind of nut the company should use to minimize the cost if 720 pounds of peanuts are available. Answer Y >X 43. The Catalog Store found that the demand equation for its Belgian waffle iron was p = -2.5x + 148, where x is the demand quantity (in thousands) and p is the price. The supply equation is p = 1.7x+43, where x is the supply quantity (in thousands) and p is the price. Find the equilibrium solution. Answer 44. Solve: (-15) (-5) - [-(-4)] - | 7= Answer 45. Translate to an algebraic equation and solve: If 8 times a certain number is increased by 5, the result is 12 times the number increased by 21. Find the number. Answer 46. Completely factor: 30xy + 35xy - 15y Answer 47. Complete the following table of equivalent forms. Write fractions in simplest terms. Show any work on the right-hand side of the page. Fractions a) 378 Decimals Percents c) -3.45 0.4%