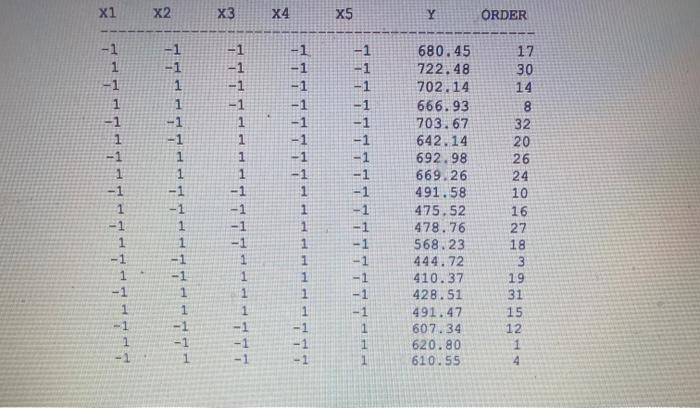
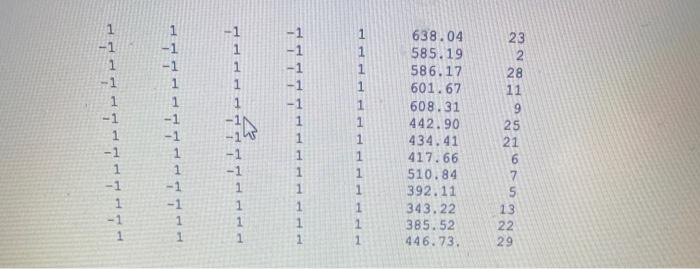
Question: (25 points) An experiment was run to determine the effect of machining factors on ceramic strength. The data variables are as follows: Response variable =

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


