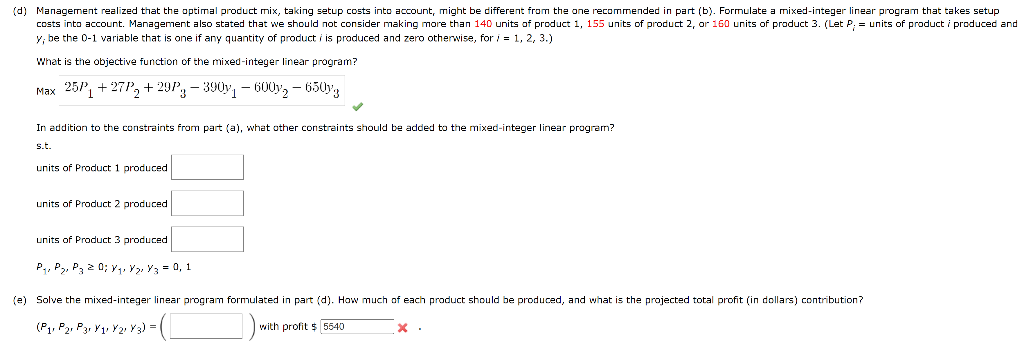
$29 far product 3. (a) Formulate a linear programming model for maximizing total profit contribution. (Let Pj= units of product i produced, for i=1,2,3.) Max25P1+27P2+29P3s.t. Department A Department B \[ \begin{array}{l} \text { Department } \mathrm { c } \longdiv { 0 . 2 5 P _ { 1 } + 0 . 2 5 P _ { 2 } + 0 . 2 5 P _ { 3 } (P1,P2,P1)=(x)withprofit$ 5 yi be the 01 variable that is one if any quantity of product i is produced and zero othervise, for i=1,2,3.) What is the objective function of the mixed-integer linear program? Max25P1+27P2+29P3390y1600y2650y3 In addition to the constraints from part (a), what ather constraints should be added to the mixed-integer linear program? s.t. units of Product 1 produced units of Product 2 produced units of Product 3 produced P1,P2,P30;y1,y2,y3=0,1 (e) Solve the mixed-integer linear program formulated in part (d). How much af each product should be produced, and what is the projected total profit (in dollars) contribution? (P1,P2,P3,y1,y2,y3)=(1