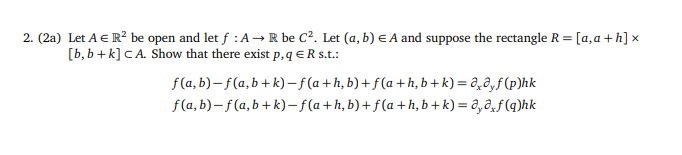
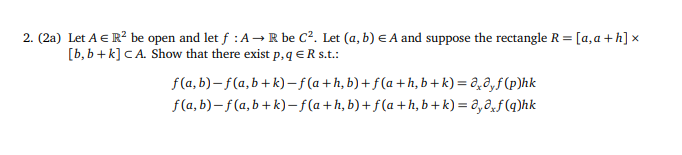
(2b) Let g : R - R be C' and a E R. Use part (a) to show that: g"(a) = lim g(ath)-2g(a) + g(a-h) h-+0 h2 (Hint: Consider f (x, y) = g(x +y).)2. (2a) Let A c R' be open and let f : A - R be C2. Let (a, b) e A and suppose the rectangle R = [a, a + h] x [b, b + k] CA. Show that there exist p, q e R s.t.: f (a, b) - f (a, b + k) - f (a + h, b) + f (a + h, b + k)= ad,f(p)hk f (a, b) - f (a, b + k) - f (a + h, b) + f (a + h, b + k) = a,a f (q)hk