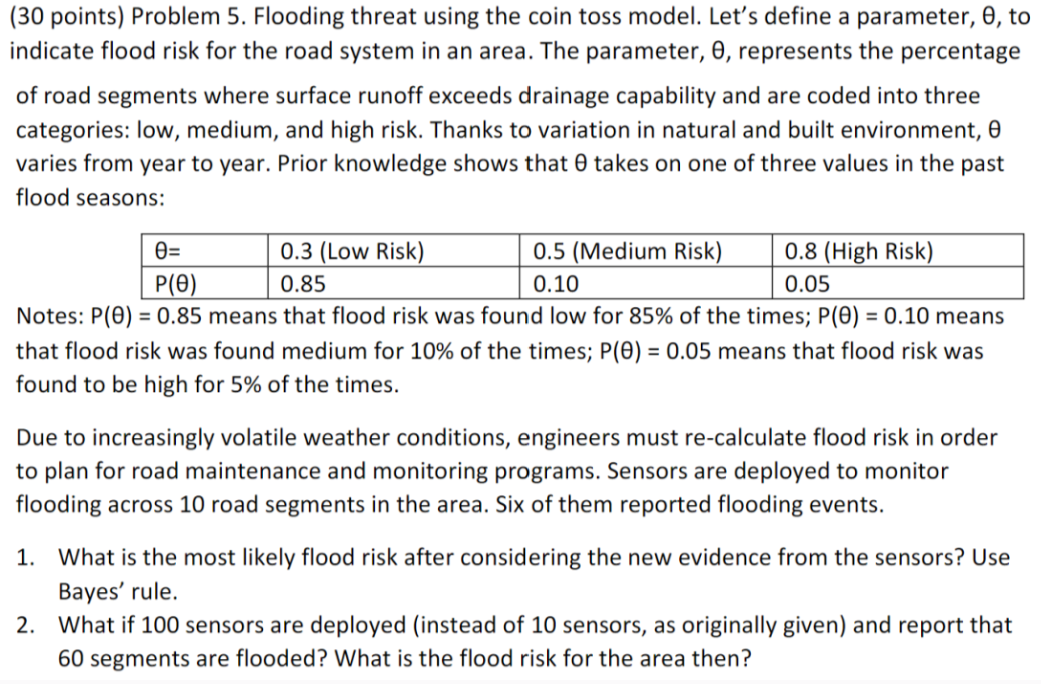
$(30$ points$)$ Problem $5.$ Flooding threat using the coin toss model. Let's define a parameter, $\backslash (\backslash$theta $\backslash ),$ to indicate flood risk for the road system in an area. The parameter, $\backslash (\backslash$theta $\backslash ),$ represents the percentage of road segments where surface runoff exceeds drainage capability and are coded into three categories: low, medium, and high risk. Thanks to variation in natural and built environment, $\backslash (\backslash$theta $\backslash )$ varies from year to year. Prior knowledge shows that $\backslash (\backslash$theta $\backslash )$ takes on one of three values in the past flood seasons:

Notes: $\backslash ($ P$(\backslash$theta$)=0\mathrm{.}85\backslash )$ means that flood risk was found low for $\backslash (85\backslash \%\backslash )$ of the times; $\backslash ($ P$(\backslash$theta$)=0\mathrm{.}10\backslash )$ means that flood risk was found medium for $\backslash (10\backslash \%\backslash )$ of the times; $\backslash ($ P$(\backslash$theta$)=0\mathrm{.}05\backslash )$ means that flood risk was found to be high for $\backslash (5\backslash \%\backslash )$ of the times.

Due to increasingly volatile weather conditions, engineers must re$-$calculate flood risk in order to plan for road maintenance and monitoring programs. Sensors are deployed to monitor flooding across $10$ road segments in the area. Six of them reported flooding events.

$1.$ What is the most likely flood risk after considering the new evidence from the sensors$?$ Use Bayes' rule.

$2.$ What if $100$ sensors are deployed $($instead of $10$ sensors$,$ as originally given$)$ and report that $60$ segments are flooded? What is the flood risk for the area then?