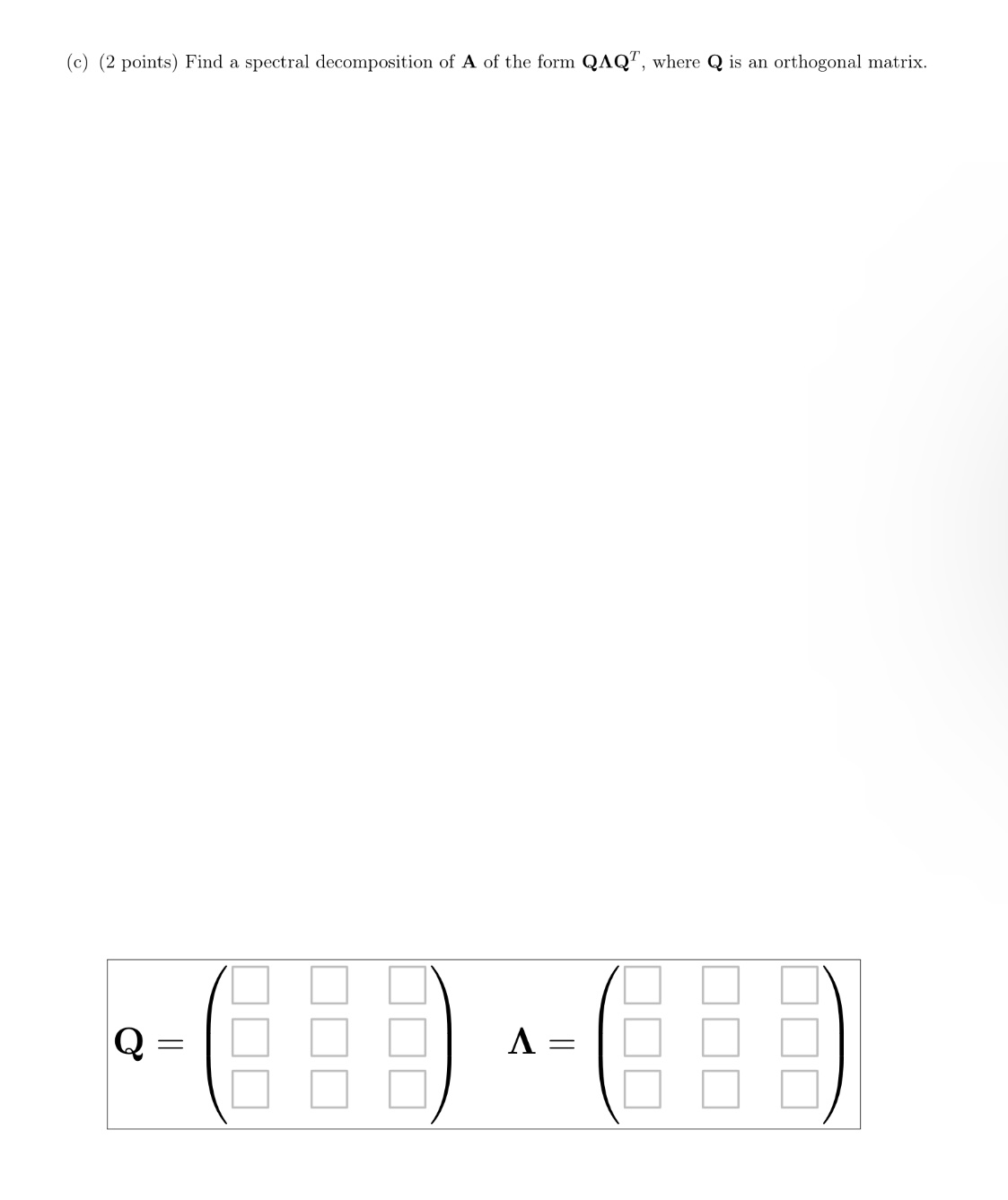
3 (5 points total) Let A 1 l 3 2 4 I} . 3 2 8 (a) (4 points) Find a basis 3;; for the nullspace of A and 21 basis 83 for the range of A. (b) (1 point] 'What is Rank(A) and Nullity(A)'.' Rank(A) = Nullity(A) : (c) (2 points) Find a spectral decomposition of A of the form QAQ", where Q is an orthogonal matrix. Q : A =4 (5 points total} Consider the following matrix: 1/2 3/2 0 A: 3/2 1/2 0 u 0 1 (a) [1.5 points) Using the characteristic polynomial. determine the eigenvalues of A. Arrange your eigenvalues so that A] 2 A2 2 A3 to ensure we all arrive at the same eenelusions in the boxes below. A1: A2: A3: (h) [1.5 points) Obtain the corresponding eigenveetors x11 X21 and x3. 5. (5 points total} Consider the matrix 2 U 2 A: 2 [J 2 U U U (a) {3 points) Obtain a. spectral decomposition for A of tho form XAX'1. 2. (5 points total) Consider the following matrix: O A = 0 2 (a) (4 points) Compute det (A) either by Laplace expansion or Gaussian elimination (your choice). det (A) = (b) (1 point) Prove the following statement or provide a counterexample: For any A, B E Rnxn, det (A? - B2) = det (A - B) det (A + B) .(b) (2 points) For r ER, the hyperbolic sine is defined as sinh (x) = ? (ex -e-x). Use your spectral decomposition from (a) to compute sinh(A). sinh (A) =