Question: 3 5 Prove Goldbach's theorem 1 = 1 3 + 1 7 + 1 8 + 1 1 5 + 1 2 4 + 1
Prove Goldbach's theorem
dots
where P is the set of "perfect powers" defined recursively as follows:
inP
Perfect power
corrupts perfectly.
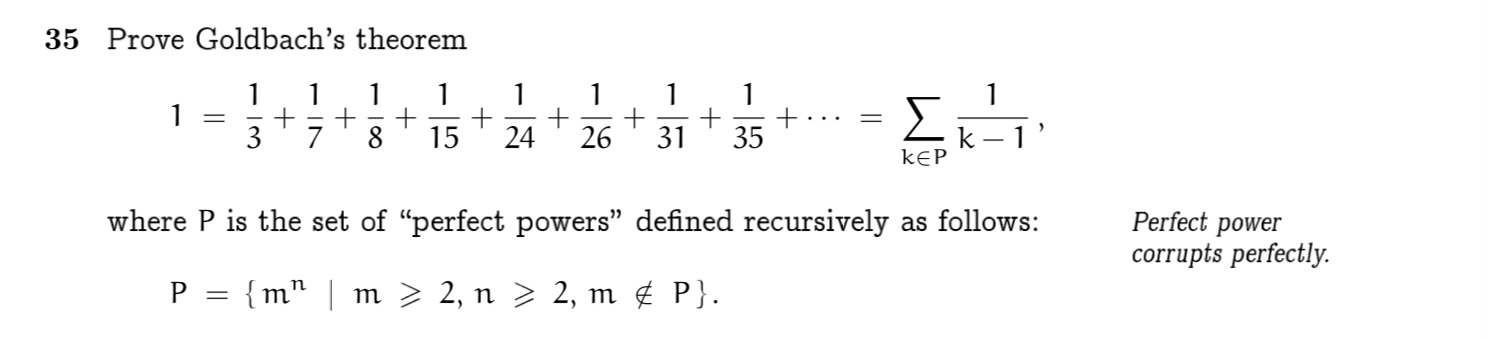
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


