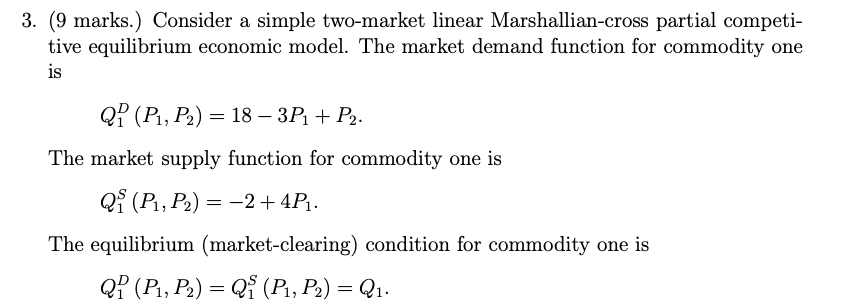
3. (9 marks.) Consider a simple two-market linear Marshallian-cross partial competi- tive equilibrium economic model. The market demand function for commodity one is QP (P1, P2) = 18 -3P1 + P2. The market supply function for commodity one is Qf (P1, P2) = -2+4P1. The equilibrium (market-clearing) condition for commodity one is QP (P1, P2) = Qi (P1, P2) = Q1.The market demand function for commodity two is (9,? {P1, P2) = 12 + P] P2. The market supply function for commodity two is Q[P1,Pg)= 2+3P2- The equilibrium [market-clearing} condition for commodity two is (9213911132): (931311132): Q2- (a) Use the equilibrium condition for commodity one and the equilibrium condition for commodity two to express this model as a system of four simultaneous linear equations in four unknown variables. {b} Express that system of four simultaneous linear equations in four unknown variables as a single augmented-row matrix. (c) Apply the process of Gauss-Jordan elimination to that augmented-row matrix to obtain its reduced row-echelon form. {d} What is the equilibrium quantity traded of commodity one, the equilibrium price of commodity one, the equilibrium quantity traded of commodity two, and the equilibrium price of commodity two