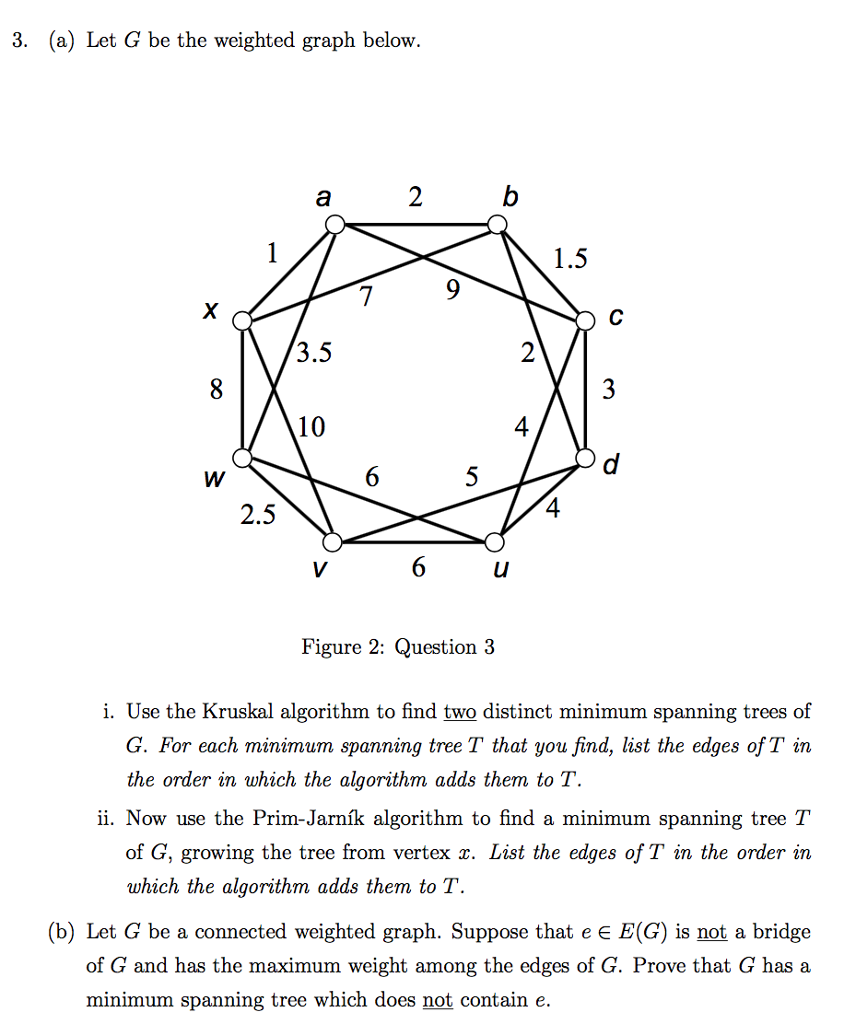
3. (a) Let G be the weighted graph below. 3.5 10 4 2.5 4 Figure 2: Question 3 i. Use the Kruskal algorithm to find two distinct minimum spanning trees of G. For each minimum spanning tree T that you find, list the edges of T in the order in which the algorithm adds them to T. ii. Now use the Prim-Jarnk algorithm to find a minimum spanning tree T of G, growing the tree from vertex x. List the edges of T in the order in which the algorithm adds them to T (b) Let G be a connected weighted graph. Suppose that e E E(G) is not a bridge of G and has the maximum weight among the edges of G. Prove that G has a minimum spanning tree which does not contain e