Question: 3. Consider the cubic iterated map In+1 = con-On. Find its equilibrium (or fixed) points and analyze their stability. Now explore using the cobweb plotting

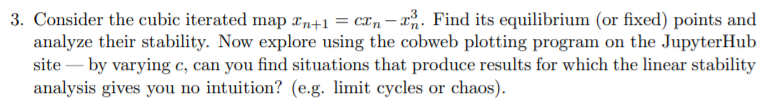
3. Consider the cubic iterated map In+1 = con-On. Find its

3. Consider the cubic iterated map In+1 = con-On. Find its equilibrium (or fixed) points and analyze their stability. Now explore using the cobweb plotting program on the JupyterHub site by varying c, can you find situations that produce results for which the linear stability analysis gives you no intuition? (e.g. limit cycles or chaos). 3. Consider the cubic iterated map In+1 = con-On. Find its equilibrium (or fixed) points and analyze their stability. Now explore using the cobweb plotting program on the JupyterHub site by varying c, can you find situations that produce results for which the linear stability analysis gives you no intuition? (e.g. limit cycles or chaos)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Calculus 3 Final answers only is okay plz highlight the final result ! \fSection 12.2: Problem 10 (1 point) Evaluate the integral by reversing the order of integration. 2 dady = by\fSection 12.2:...

please answer part 3 Consider the following game, where player 1 chooses a strategy U or M or D and player 2 chooses a strategy L or R. 1. (2 points) Under what conditions on the parameters is U a...

Consider the following cubic polynomial equation. N 275 + 1622% + 108z 755 = 0 By dividing both sides of the equation by 27, convert this to a monic polynomial equation. a Using the method described...

Can you solve the following questions and provided a detailed explanation. Thank you!:) 1. Evaluate the integral [/4cos($)y3 dA Where R = {(9:44) : 0 3 cc 3 725,0 3 y S 1}. R 2. Evaluate the integral...

2 is possible that some firms do not produce in a PE allocation. What can be said about which firms they are? c. Compare the levels of food consumption by different consumers in a given PE...

3. Consider the networks shown in the figure below. There are two user machines ml.a.com and m2.a.com in the network a.com. Suppose the user at ml.a.com types in the URL www.b.com/bigfile.html into a...

explain all parts of the question with step by step 2. There are two goods, food and clothing, whose quantities are denoted by I and y and prices by ps and py, respectively. There is a consumer whose...

3. Consider the following diagram that shows how the web server's IP address can be found from the requesting host by using the DNS service. In this scenario, find out the total delay from the time...

i need the answers for a, b and c please Let y, ..., yn be a set of responses and let x1, ...,an be a corresponding set of predictors lying in the interval [a, b]. Recall that a cubic smoothing...

Question 3 Consider the following discrete choice game in which two coffee shops must simultaneously choose their pricing strategy. There are two coffee shops in a nearby business district, with...

Consider a system of N non-interacting particles confined in a volume V at a temperature such that the particles obey classical Boltzmann statistics. If the temperature is lowered to the point at...

You are the payables accountant for a medium-sized electrical contracting company. You are paying bills with purchase discounts but can't take advantage of them because the cash balance in the...

A company has annual fixed costs of $ 1 , 2 9 5 , 0 0 0 and variable costs of $ 0 . 5 0 / unit produced. To breakeven, the company charges $ 6 per unit. How many units does the company produce each...

Statement of Cash Flows The comparative balance sheet of Orange Angel Enterprises Inc. at December 3 1 , 2 0 Y 8 and 2 0 Y 7 , is as follows: Dec. 3 1 , 2 0 Y 8 Dec. 3 1 , 2 0 Y 7 Liabilities and...

4. Who should be invited to attend?

7. How will you encourage her to report back on the findings?

Were the decisions based on appropriate facts?