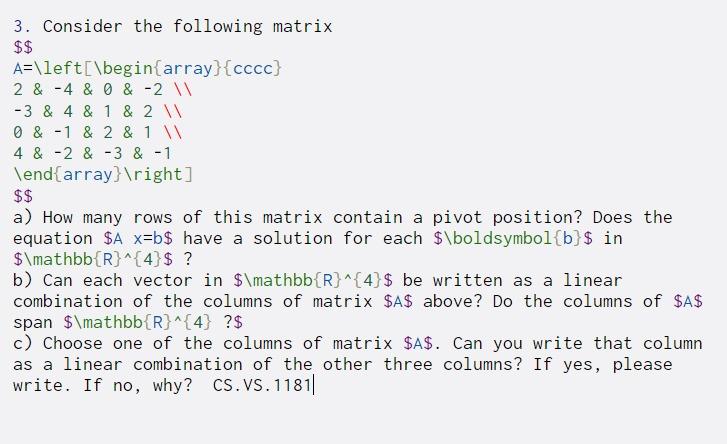
3. Consider the following matrix $$ A=\left[\begin{array}{cccc} 2 & -4 & 0& -2 -3 & 4 & 1 & 2 0 & -1 & 2 & 1 W 4 & -2 & -3 & -1 \end{array} ight] $$ a) How many rows of this matrix contain a pivot position? Does the equation $A x=b$ have a solution for each $\boldsymbol{b}$ in $\mathbb{R}^{4}$ ? b) Can each vector in $\mathbb{R}^{4}$ be written as a linear combination of the columns of matrix $A$ above? Do the columns of $A$ span $\mathbb{R}^{4} ?$ c) Choose one of the columns of matrix $A$. Can you write that column as a linear combination of the other three columns? If yes, please write. If no, why? CS.VS. 1181||