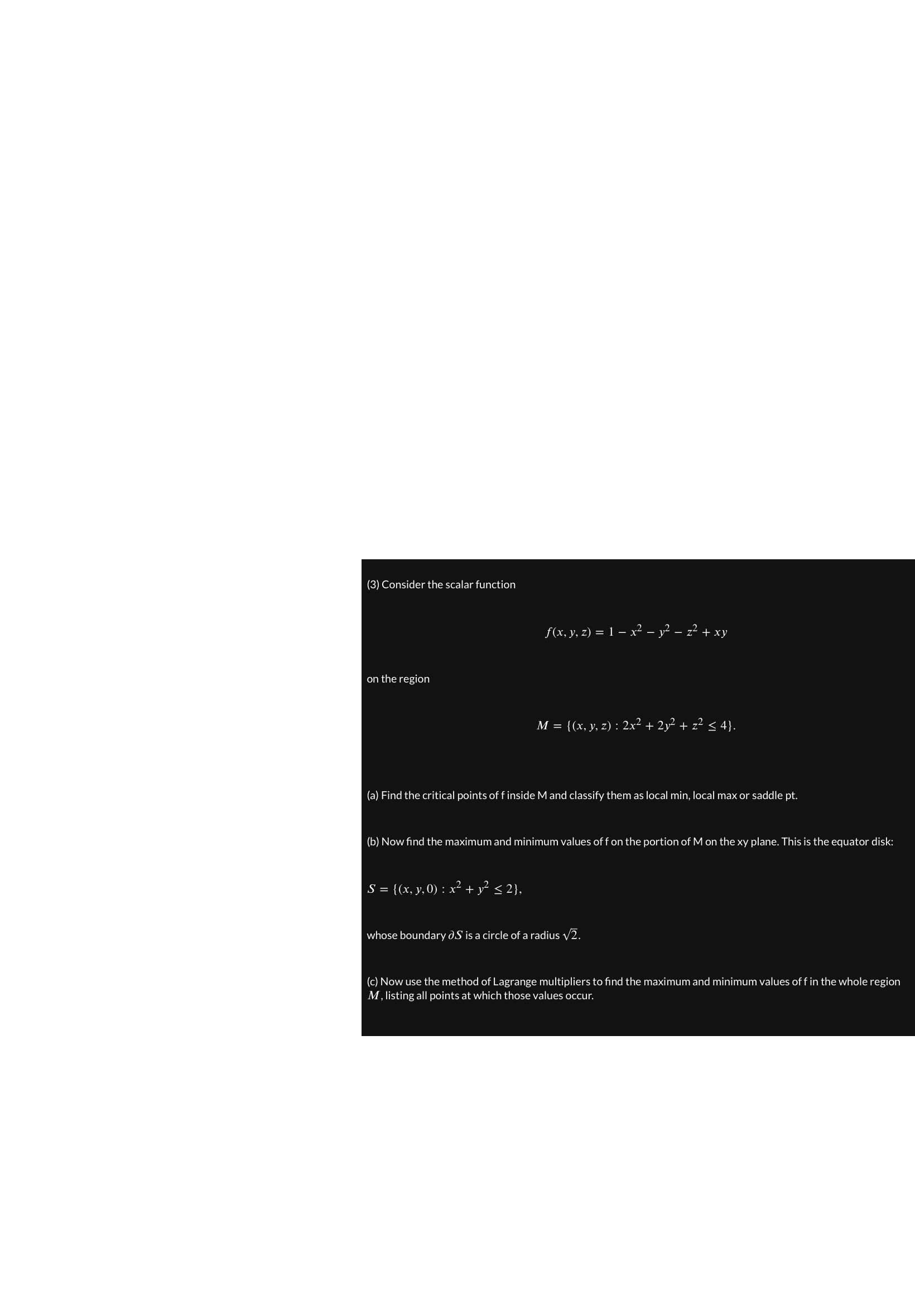
(3) Consider the scalar function f(x, y, z) = 1 - x2 - y2 - z2 + xy on the region M = ((x, y, z) : 2x2 + 2y2+ 22 s 4). (a) Find the critical points of f inside M and classify them as local min, local max or saddle pt. (b) Now find the maximum and minimum values of f on the portion of M on the xy plane. This is the equator disk: S = { (x, y. 0) : x2 + 12 s 2). whose boundary OS is a circle of a radius v2. (c) Now use the method of Lagrange multipliers to find the maximum and minimum values of f in the whole region M, listing all points at which those values occur