Question: 3. Define M = 0 0 0 0 3 -1 0-1 3 (a) Name an easily observable property of the matrix M that guarantees

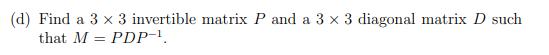
3. Define M = 0 0 0 0 3 -1 0-1 3 (a) Name an easily observable property of the matrix M that guarantees that it is diagonalizable. (b) Compute the characteristic polynomial PM(A) of M and find all its zeros. (c) Find a basis of R3 consisting of eigenvectors of M. (d) Find a 3 x 3 invertible matrix P and a 3 x 3 diagonal matrix D such that M PDP-. =

Step by Step Solution

★★★★★

3.34 Rating (145 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Find a diagonalizable matrix A such that D + A is not diagonalizable. If 0 -1

find an invertible matrix P and a matrix C of the form such that A = PCP -1 . Sketch the first six points of the trajectory for the dynamical system and classify the origin as a spiral attractor,...

Find an invertible matrix P and a matrix C of the form such that A = PCP -1 . Sketch the first six points of the trajectory for the dynamical system and classify the origin as a spiral attractor,...

State at least three (3) roles of the geodetic engineers in the following government agencies: 1. Land Management Bureau and DENR Regional Offices 2. Department of Land Reform 3. National Mapping and...

Python and most Python libraries are free to download or use, though many users use Python through a paid service. Paid services help IT organizations manage the risks associated with the use of...

Question 1 10 pts What is the characteristic polynomial for 5 Ox2 + d + 2 0 12 - X+ 2 0 12 - 1 - 2 O x2 + 1 - 2 Question 2 21 pts -1 1 -1 O O 0 -1 1 1 3 HN 0 -1 0 For A = 0 0 OHO 0 OON ONO o o O ....

Please do this in c++. DO NOT DO THIS IN JAVA OR OTHER LANGUAGES. Important: use recursion to implement DFS. Write a C++ or Java class definition for an abstract data type called Graph that models an...

Can you please help me with number 21. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! Open with Chapter 5 Linear Systems...

Note: This problem is for the 2019 tax year. Alfred E. Old and Beulah A. Crane, each age 42, married on September 7, 2017. Alfred and Beulah will file a joint return for 2019. Alfred's Social...

Below are three documents the two excel worksheets are complete they are just there to help answer the questions in the word document. SO basically all i need help on is the word document, answering...

A company has just paid a dividend of 3.7$. Its discount rate is 8.8%, and the expected perpetual growth rate is 3.1%. What would you expect to be the stock's price IN ONE YEAR?

Consider the following 27-periodic function: = { Note that the 27-periodicity of the above function essentially says that f() := f(-) = 0. f(x): for x [-7,0) for x = [0, ) (2a) Find the Fourier...

Use the Ratio Test to determine the interval of convergence of \ sum _ ( n = 1 ) ^ ( \ infty ) ( x ^ ( n ) ) / ( \ root ( 1 2 ) ( n ) * 4 ^ ( n ) ) * , * \ infty for infinity, u for combining...

Strassel Investors buys real estate, develops it, and resells it for a profit. Anew property is available, and Bud Strassel, the president and owner of Strassel Investors, believes it can be sold for...

In Problem 14.3 on page 582, you predicted the durability of a brand of running shoe, based on the forefoot shock-absorbing capability (FOREIMP) and the change in impact properties over time...

Use the following information from a multiple regression model: n = 20 b 1 = 4 b 2 = 3 S bi = 1.2 Sb 2 = 0.8 a. Which variable has the largest slope, in units of a t statistic? b. Construct a 95%...

According to a summary of the payroll of Murtagh Co., $750,000 was subject to the 6.0% social security tax and the 1.5% Medicare tax. Also, $50,000 was subject to state and federa unemployment taxes....

Kent, CPA, is the engagement partner on the financial statement audit of Super Computer Services Co. (SCS) for the year ended April 30, 2011. On May 6, 2011, Smith, the senior auditor assigned to the...

What is the value of the standardized test statistic? The standardized test statistic is negative 3.19. (Round to two decimal places as needed.) Part 3 What is the P-value? Pequals enter your...

Mary paid $2,000 of state income taxes in 2012. The total sales tax she paid during 2012 was $5,500, which included $3,000 for the cost of a new car. How should Mary treat the taxes paid on her 2012...

Your supervisor has asked you to research the following situation concerning Owen and Lisa Cordoncillo. Owen and Lisa are brother and sister. In May 2012, Owen and Lisa exchange business pickup...

Janie graduates from high school in 2012 and enrolls in college in the fall. Her parents pay $4,000 for her tuition and fees. a. Assuming Janie's parents have AGI of $170,000, what is the American...

Following are the quantities and prices for the years 2000 and 2014 for Kinzua Valley Geriatrics. Use 2000 as the base period. a. Determine the simple price indexes. b. Determine the simple aggregate...

The production manager of MPS Audio Systems Inc. is concerned about the idle time of workers. In particular, he would like to know if there is a difference in the idle minutes for workers on the day...

Refer to the data on the school buses in the Buena School District. a. Assume the distribution of the maintenance cost for the three bus manufacturers does not follow a normal distribution. Conduct a...