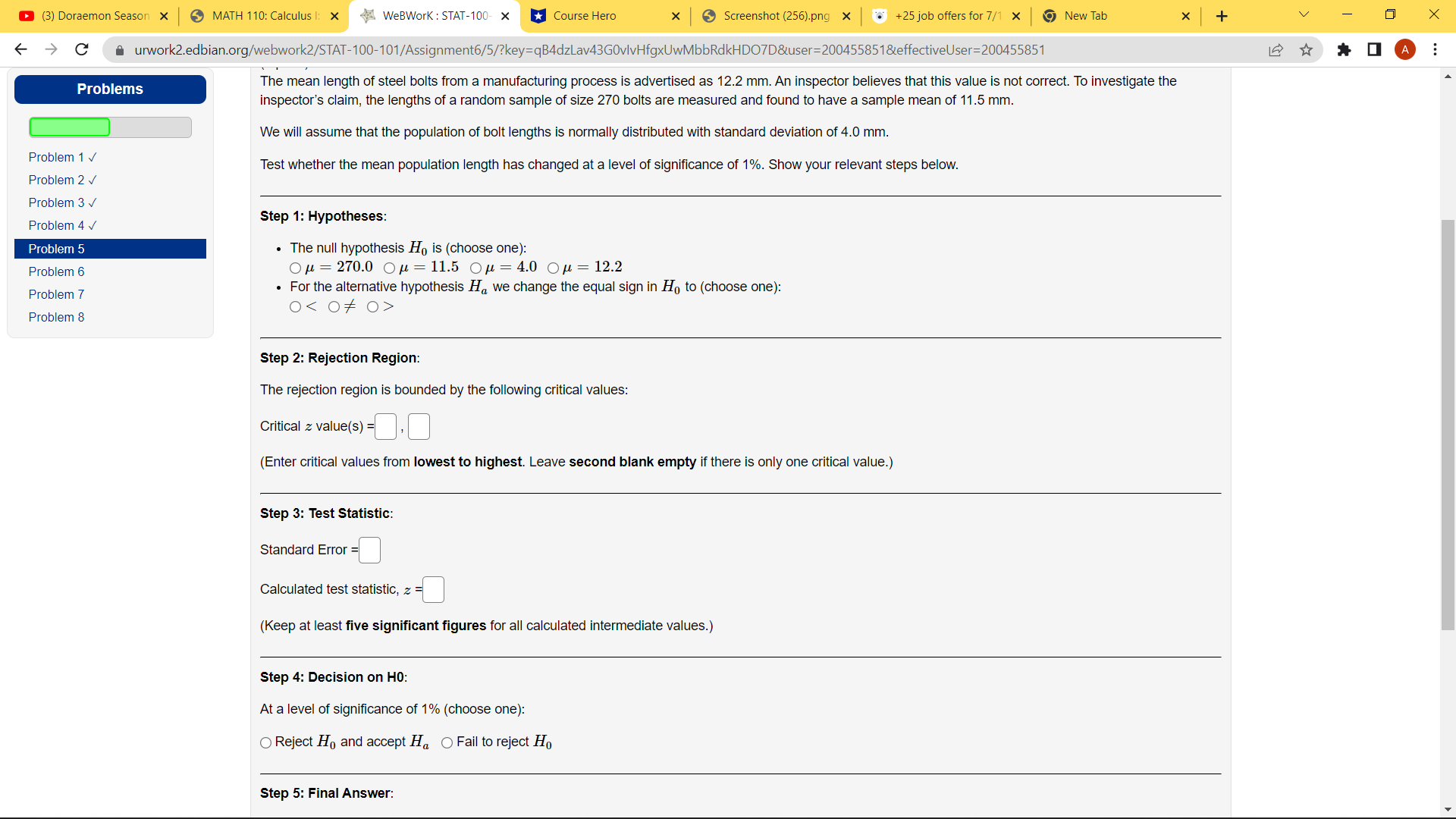
(3) Doraemon Season X MATH 110: Calculus |: X WeBWork : STAT-100- X Course Hero Screenshot (256).png x +25 job offers for 7/1 x New Tab X + V X - > C a urwork2.edbian.org/webwork2/STAT-100-101/Assignment6/5/?key=qB4dzLav43GOvlvHfgxUwMbbRdkHDO7D&user=200455851&effectiveUser=200455851 * Problems The mean length of steel bolts from a manufacturing process is advertised as 12.2 mm. An inspector believes that this value is not correct. To investigate the inspector's claim, the lengths of a random sample of size 270 bolts are measured and found to have a sample mean of 11.5 mm. We will assume that the population of bolt lengths is normally distributed with standard deviation of 4.0 mm. Problem 1 v Test whether the mean population length has changed at a level of significance of 1%. Show your relevant steps below. Problem 2 V Problem 3 V Problem 4 V Step 1: Hypotheses: Problem 5 . The null hypothesis Ho is (choose one): Problem 6 OH = 270.0 Of = 11.5 Ou = 4.0 Ou = 12.2 Problem 7 For the alternative hypothesis Ha we change the equal sign in Ho to (choose one): 0 Problem 8 Step 2: Rejection Region: The rejection region is bounded by the following critical values: Critical z value(s) =. (Enter critical values from lowest to highest. Leave second blank empty if there is only one critical value.) Step 3: Test Statistic: Standard Error = Calculated test statistic, z = (Keep at least five significant figures for all calculated intermediate values.) Step 4: Decision on HO: At a level of significance of 1% (choose one): O Reject Ho and accept Ha O Fail to reject Ho Step 5: Final