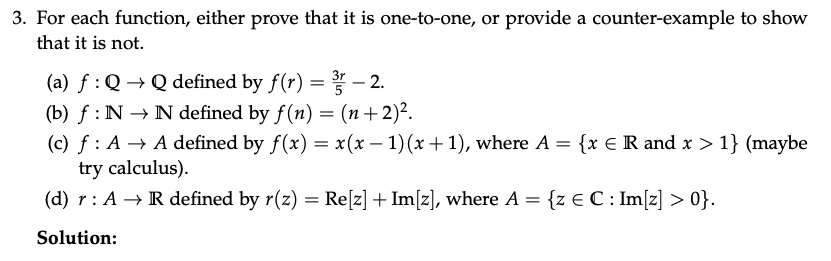
3. For each function, either prove that it is one-to-one, or provide a counter-example to show that it is not. (a) f : Q - Q defined by f(r) = ; - 2. (b) f : N - N defined by f (n) = (n+ 2)2. (c) f : A - A defined by f(x) = x(x - 1) (x + 1), where A = {x E R and x > 1} (maybe try calculus). (d) r : A - R defined by r(z) = Re[z] + Im[z], where A = {z E C : Im[z] > 0}. Solution