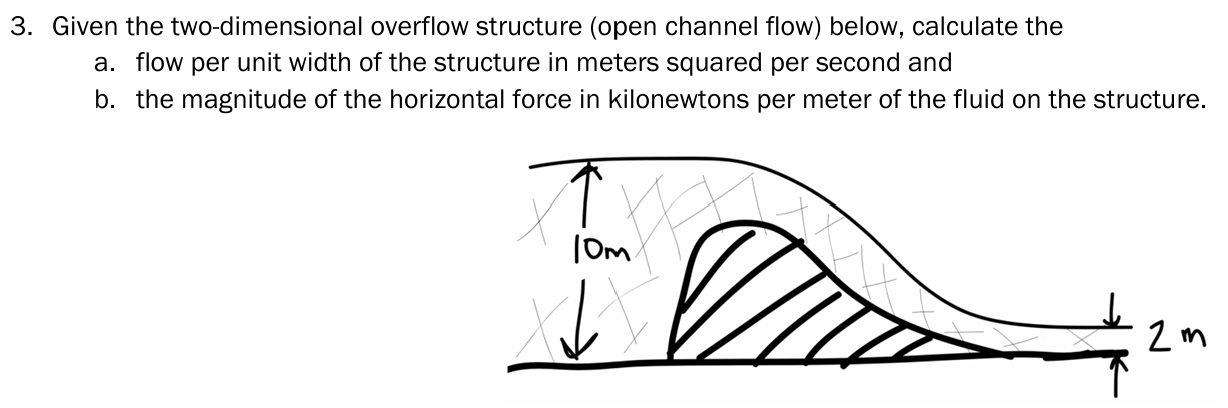
Question: 3 . Given the two - dimensional overflow structure ( open channel flow ) below, calculate the a . flow per unit width of the
Given the twodimensional overflow structure open channel flow below, calculate the
a flow per unit width of the structure in meters squared per second and
b the magnitude of the horizontal force in kilonewtons per meter of the fluid on the structure.
Formulas
sgrho subrho Hogamma water lbfftgamma water Nmgamma rho ggmsfts
tau mu dvdymu rho
u patm psi kPa,RLPa Kmol
u water times ms at deg Ctimes ftss at deg F
Fgamma hcAypycIcycARerho vLmu vL
u QvaPVmRT
Pgamma zvgPgamma zvgH gallons ftlbflbmfts
Pgamma zvghuPgamma zvghehlPgamma Qhuhorsepowergamma Qhukilowatts
sum vecFext rho QvecVvecVsum Fxrho QVxVxsum Fyrho QVyVy
a nectangre
Api RItimes CR
Api abItimes Cab
d Triangle
e Semicircle
f Semiellipse
Figure of Cengel
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


