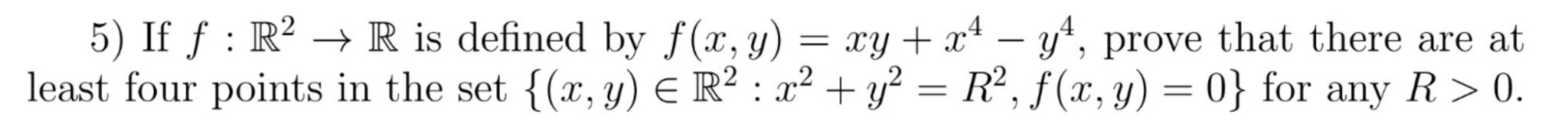
3) Let f RR be defined to be zero on the irrational numbers, and for a rational number x Q, write x as x = p/q where p = Z, q = N and GCD(p, q) = 1 and define f(x) = 1/q. Prove that the set of points where f is continuous is precisely the irrational numbers. Saying that GCD(p,q) = Context: 1 is equivalent to say p and q have no common divisors, i.e. if a prime divides p then it does not divide q. Every rational number has a unique representation as 2 with GCD(p,q) = 1, but notice if you allow common divisors then the representation is not unique 3 = = 0, etc. q = 6 6 9 - 5) If : R R is defined by f(x, y) = xy + x y, prove that there are at least four points in the set {(x, y) = R : x + y = R, f(x, y) = 0} for any R > 0. For problem (5) you can assume that the functions sin, cos: R R exist and satisfy the standard properties of these trigonometric functions, i.e. that they are continuous, sin (x) + cos (x) = 1, and that the function x (cos(x), sin(x)) has sin(x) cos(x) image the unit circle, in particular the image of [0,2] is the unit circle.