Question: 3. Let f(x) be a nonnegative, integrable function on [0, 1] with f(0) = f(1) = 0. Suppose that f is differentiable at every point

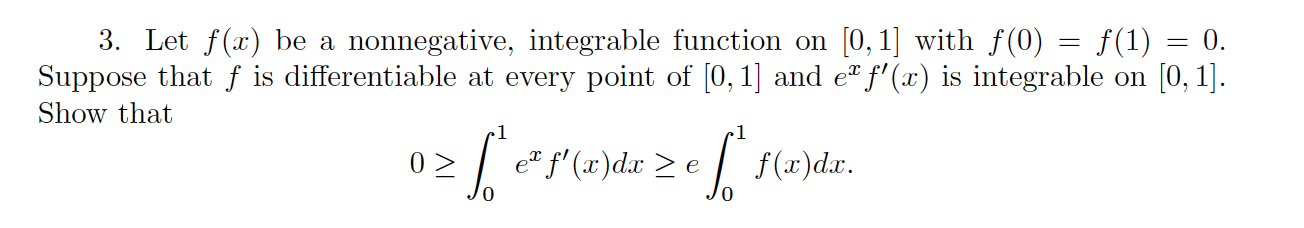
3. Let f(x) be a nonnegative, integrable function on [0, 1] with f(0) = f(1) = 0. Suppose that f is differentiable at every point of [0, 1] and ex f'(x) is integrable on [0, 1]. Show that 0Z er f'(x)dx z e f(x) dx. 0

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Let f(x) be a real-valued Lebesgue integrable function on [0, 1]. (a) Prove that if f> 0 on a set F C [0, 1] of positive measure, then (b) Prove that if [ f(x) dx > 0. F [ f(x) dx = 0, then f(x) = 0...

Section 4.1: (page 247) Numbers 1, 3, 7-13 odd, 19-23 odd Section 4.2: (page 260) Numbers 1, 5, 13, 19a, 20a Section 4.3: (page 270) Numbers 1-5 odd textbroker.com X Final Exam X X Canvas LMS X...

4 ECE 5759 Problem 1. Due: October 25 Closed Convex set in the space of Matrices (10 marks) nn A matrix A R is called a positive semidefinite matrix if xT Ax 0 for every x Rn . Prove that the set of...

Let f (x , y ] =. 1x4/5/4 it (L , y ) + (0 .0 ) 0 -, if ( x , y ) = ( 010 ) 5 ) A function f: IRh, In is said to be even, complete if fox) = PC-x ) v x ERS. If pes differentiable () and even Compute...

8249 (course MATH 132-c03 Busin... Previous Problem Problem List Next Problem 06 - Rates Slopes and Derivatives: Problem 13 (1 point) Instructions: For the remainder of the problems in this...

AP Calculus Question 2. Let f (x) be a twice differentiable function for all real numbers. The table on the right gives values of x 4 f (x) for selected points in the closed interval f (x) l S x S 1...

Homework 4 Score: 0/70 0/7 answered Question 1 The graph of f(x) is shown below. Estimate and list the value of x where f(x) has a horizontal tangent. 10 -9 -8 -7 -6 -5 4 -3 - 2 -7 1 2 3 4 5 6 7 8 9...

STAT 67, Fall 2016 Homework 4 11-10-2016 1. You are waiting for the bus to arrive to pick you up. You believe the wait time can be any number between 0 and 5 minutes, with uniform density. a. What is...

#1. Please help! Show work please DIRECTIONS: To receive full credit, make sure your work is neat and complete. 1. (a) Let f(x) = ax + b, where a # 0. Prove the x-intercept of the graph of f happens...

Characterize the following compounds as soluble or insoluble in water: (a) Ca3(PO4)2 , (b) Mn(OH)2 , (c) AgClO3, (d) K2S.

A comparable property sold 4 months ago for $265,500. The adjustments for the various elements of comparison have been calculated as follows: Location: +4% Market conditions: +0.2% per month...

Consider the data in Exercise 8.2, find (a) the range; (b) the standard deviation.

Please help it's urgent thank you. please write 400-450 words. thank you QUESTION 4 (20 MARKS) The success of any project is dependent on a diverse range of skills, abilities and competencies of the...

10. First test yourself and then let another member of the group test you in relation to the following questions. If deviations occur, discuss why this might be. What can the results of this test be...

5. Based on your desired future, answer the following questions: (a) What do you want, i.e. what goals have you set yourself? Set up three goals in order of priority. (b) Why do you want this? (c)...

1. Discuss the following statements: (a) Its what you are best at that will be your downfall. (b) How can we learn but not learn? (c) Learning to see is different from seeing. (d) Creativity is...