Question: 3. Let G (V, E) be a simple undirected connected graph with n vertices. The BFS and the DFS traversals generate rooted and ordered traversal

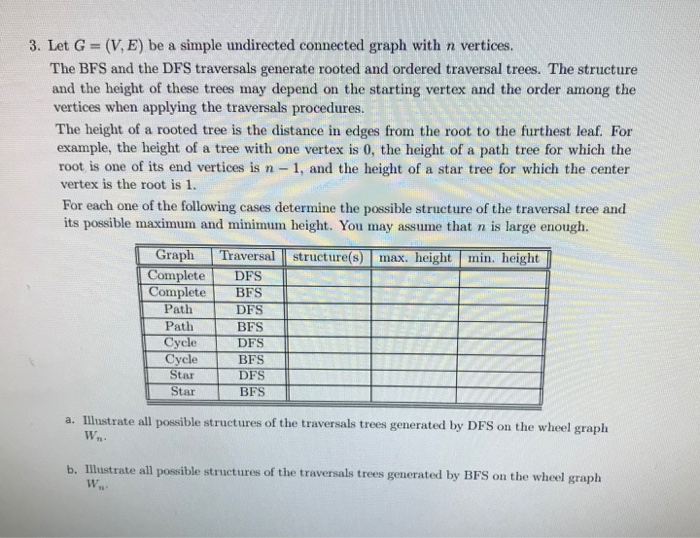
3. Let G (V, E) be a simple undirected connected graph with n vertices. The BFS and the DFS traversals generate rooted and ordered traversal trees. The structure and the height of these trees may depend on the starting vertex and the order among the vertices when applying the traversals procedures. The height of a rooted tree is the distance in edges from the root to the furthest leaf. For example, the height of a tree with one vertex is 0, the height of a path tree for which the root is one of its end vertices is n -1, and the height of a star tree for which the center vertex is the root is 1. For each one of the following cases determine the possible structure of the traversal tree and its possible maximum and minimum height. You may assume that n is large enough. Graph Traversal structure(s) max. height min height Complete DFS Complete BFS DFS Path Path BFS Cycle DFS Cycle Star Star BFS DFS BFS a. Illiustrate all possible structures of the traversals trees generated by DFS on the wheel graph Wn. b. IIlistrate all possible structures of the traversals trees generated by BFS on the wheel graph W

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

For a graph, n and m denote number of vertices and edges respectively. 1. Write the pseudo code for Depth First Search of G, provided the Adjacency list is used. 2. Let G = (V,E ) be a graph. Outline...

Need help 5. (25 pts.) Circle True or False (no justification needed). a) Any connected graph on n vertices has n-1 edges. True False b) Chromatic number of a graph is always the minimum degree + 1....

Let G = (V, E) be a connected, undirected graph. (In this course we follow the usual convention that, unless indicated otherwise, an undirected graph does not have loops or multiple edges.) As usual...

1: Suppose G = (V, E) is a simple graph (no self-loops or multiple edges). The degree sequence of G is 1, 3, 3, 4, 5. What is the number of edges in G? Problem 2: Suppose T is a tree on 6 vertices...

Why is there a depletion layer in the immediate vicinity of the junction? 1 [TURN OVER CST.93.1.2 SECTION B 5 Give an ML definition of the function map3 which has the property that map3 f [x1, x2, ....

ANSI-SPARC6 Programming Language Compilation Write notes on each of the following topics: (a) the implementation of labels and jumps in a recursive, block structured programming language [7 marks]...

Deduce the type of map3iter and explain in words what the function does. Illustrate your answer by considering the call map3iter g [1, 1, 1, 1, 1, 1]; in an environment in which g is defined as...

nodes, but at least its bias can be quantified by Markov Chain L. INTRODUCTION analysis and thus can be corrected via appropriate re-weighting The popularity of online social networks (OSNs) in...

Write a C + + Program following these instructions: - "palomarMapEdge.txt " data format: ID , building name, x & y coordinates ( use for vertex ) , and then all the adjacent vertices / buildings that...

Under the entity approach of reporting non-controlling interest, what value is assigned to goodwill?

A balance sheet of Brown University, issued prior to the effective date of FASB Statement No. 117, is presented below. Recast the fund balance (net asset) section of the balance sheet so that it...

Help Asap. Draw a tangent from the risk - free rate to the opportunity set. What does your graph show for the expected return and standard deviation of the optimal risky portfolio? ( LO 6 - 3 ) What...

A company is preparing completing their Cash Budget. The following data has been prepared for cash receipts and payments. January February March Cash receipts $1,061,200 $1,182,400 $1,091,700 Cash...