Question: 3) Let m = i=1 where p1 2 be an integer, and denote by [x] the congruence class of r E Z modulo n. (i)
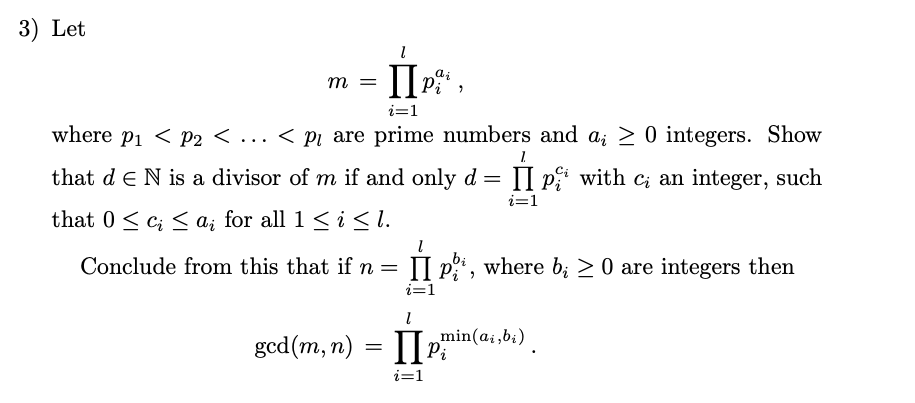
![and denote by [x] the congruence class of r E Z modulo](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6709ae76731ce_7346709ae76643ac.jpg)
3) Let m = i=1 where p1 2 be an integer, and denote by [x] the congruence class of r E Z modulo n. (i) The sets [0], [1], ..., [n - 1] are all congruence classes modulo n. We have [i] n[i] = 0 for all i # j in the set {0, . .., n - 1} and n-1 Z = [ , 1=0 i.e. Z is the disjoint union of the congruence classes [0], . . ., [n - 1]. (ii) The following three statements are equivalent for all integers a, be Z: (a) [a] = [b]; (b) [a]n [b] # 0; and (c) a = b mod n
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


