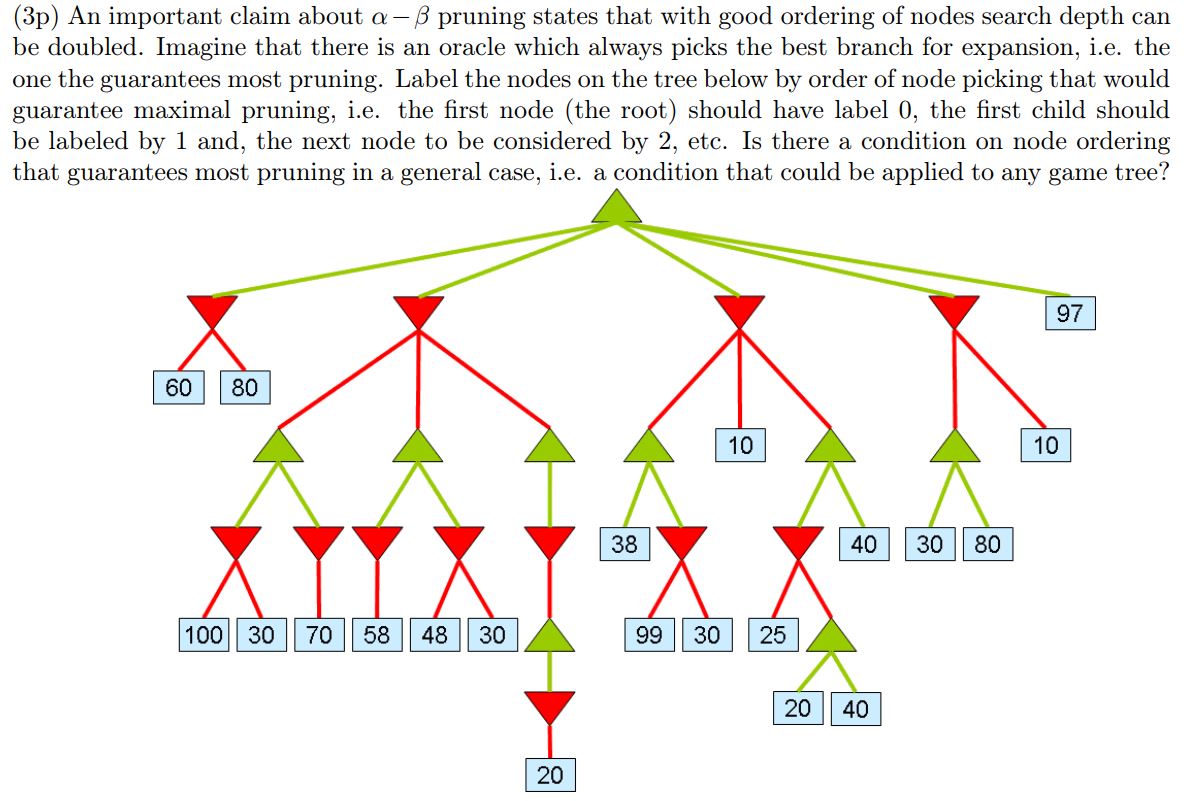
$(3$p$)$ An important claim about $\backslash (\backslash$alpha$-\backslash$beta $\backslash )$ pruning states that with good ordering of nodes search depth can be doubled. Imagine that there is an oracle which always picks the best branch for expansion, i$.$e$.$ the one the guarantees most pruning. Label the nodes on the tree below by order of node picking that would guarantee maximal pruning, i$.$e$.$ the first node $($the root$)$ should have label $0,$ the first child should be labeled by $1$ and, the next node to be considered by $2,$ etc. Is there a condition on node ordering that guarantees most pruning in a general case, i$.$e$.$ a condition that could be applied to any game tree? $(2$p$)$ Apply minimax with right to left alpha$-$beta pruning on the following graph. Show the backed up values, the places where alpha$-$beta prunes $($the cuts$)$ and the reason for each cut. Reasons can be simple $($i$.$e$.,"\backslash (8<mn>1</mn><mn>5</mn><mtext></mtext><mi>\backslash </mi><mi>)</mi><mtext></mtext><mi>"</mi>$ or $"\backslash (12>6\backslash )").$ Please note that the solution for left to right pruning can be found on the blackboard under "Alpha$-$Beta Pruning Example". $(2$p$)$ In the simple tree below

the MAX is playing an opponent who plays rationally $($Minimax$)\backslash (50\backslash \%\backslash )$ of the time, but acts randomly for the remaining $\backslash (50\backslash \%\backslash ).$ For what values of $\backslash ($ x $\backslash )$ should the $\backslash ($ M A X $\backslash )$ player pick the left branch? Are there any values of $\backslash ($ x $\backslash )$ for which the MAX should pick the right branch? Hint: Whichever branch the MAX picks $\backslash (50\backslash \%\backslash )$ of the the outcome is given by the Minimax, while $\backslash (50\backslash \%\backslash )$ of the time it is given by Expectimax. $(3$p$)$ A simple version of a "Grundy's game" is played as follows: Two players have in front of them a single pile of objects, say a stack of $6$ pennies. The first player divides the original stack into two stacks that must be unequal. Each player alternatively thereafter does the same to some single stack when it is his turn to play. The game proceeds until each stack has either just one penny or two$-$at which point continuation becomes impossible. The player who first cannot play is the loser. Show, by drawing a game tree, whether any of the players can always win.