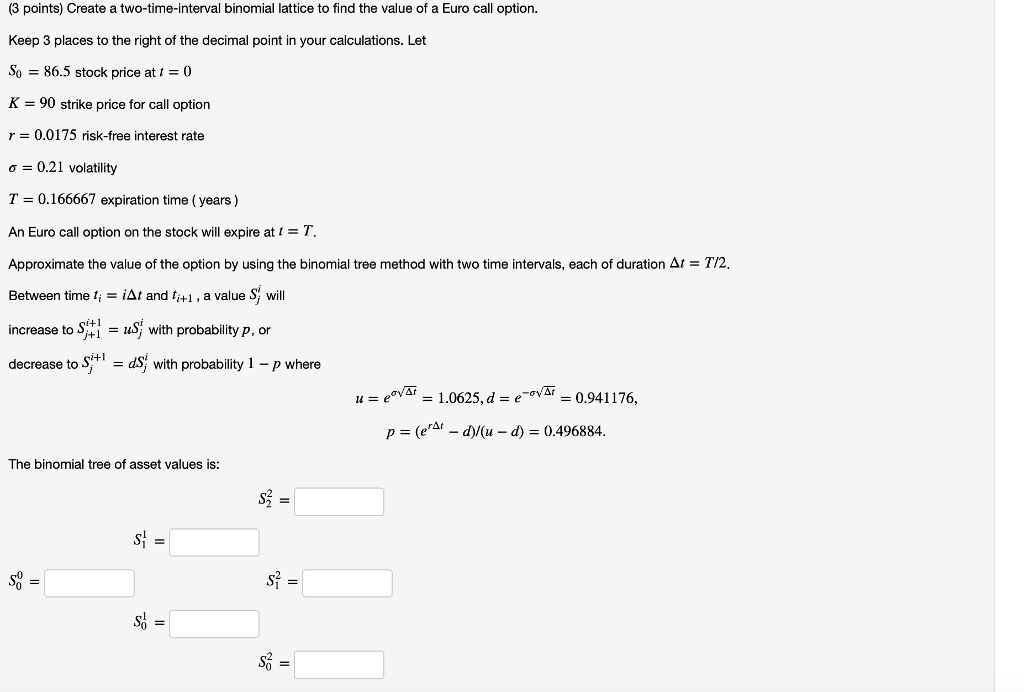
(3 points) Create a two-time-interval binomial lattice to find the value of a Euro call option. Keep 3 places to the right of the decimal point in your calculations. Let So 86.5 stock price at -0 K 90 strike price for call option r 0.0175 risk-free interest rate = 0.21 volatility T = 0.166667 expiration time ( years ) An Euro call option on the stock will expire at t- T. Approximate the value of the option by using the binomial tree method with two time intervals, each of duration 1-T72 Between time ti-1 and ti+1 , a value S1 will increase to SjuS with probability p, or decrease to S+with probability 1 -p where i+1 u = eo r = 1.0625, d = e-ova 0.941176, p - (er - d)/(u - d)- 0.496884 The binomial tree of asset values is: So The binomial tree of European call option values is V. V, 0 0 From the Black-Scholes formula, the true value of the Euro call option is Euro Hint: Google "Black-Scholes calculator online" and use one such as the ERI calculator that allows entering time to expiration in years. The error in using the binomial lattice method rather than Black-Scholes is the value C-Euro-VO- (3 points) Create a two-time-interval binomial lattice to find the value of a Euro call option. Keep 3 places to the right of the decimal point in your calculations. Let So 86.5 stock price at -0 K 90 strike price for call option r 0.0175 risk-free interest rate = 0.21 volatility T = 0.166667 expiration time ( years ) An Euro call option on the stock will expire at t- T. Approximate the value of the option by using the binomial tree method with two time intervals, each of duration 1-T72 Between time ti-1 and ti+1 , a value S1 will increase to SjuS with probability p, or decrease to S+with probability 1 -p where i+1 u = eo r = 1.0625, d = e-ova 0.941176, p - (er - d)/(u - d)- 0.496884 The binomial tree of asset values is: So The binomial tree of European call option values is V. V, 0 0 From the Black-Scholes formula, the true value of the Euro call option is Euro Hint: Google "Black-Scholes calculator online" and use one such as the ERI calculator that allows entering time to expiration in years. The error in using the binomial lattice method rather than Black-Scholes is the value C-Euro-VO