(3 points) Let

A_(1),A_(2),dots

be sets such that for each

n

we have

\\\\cap n_(i)=1^(n)A_(i)!=(O)/()

. Is it possible\ for

\\\\cap n_(i)=1^(\\\\infty )A_(i)=(O)/()

? (In order to receive credit you must either demonstrate an example\ that shows that it is possible that

\\\\cap n_(i)=1^(\\\\infty )A_(i)=(O)/()

, or prove that there cannot exist such\ sets.)

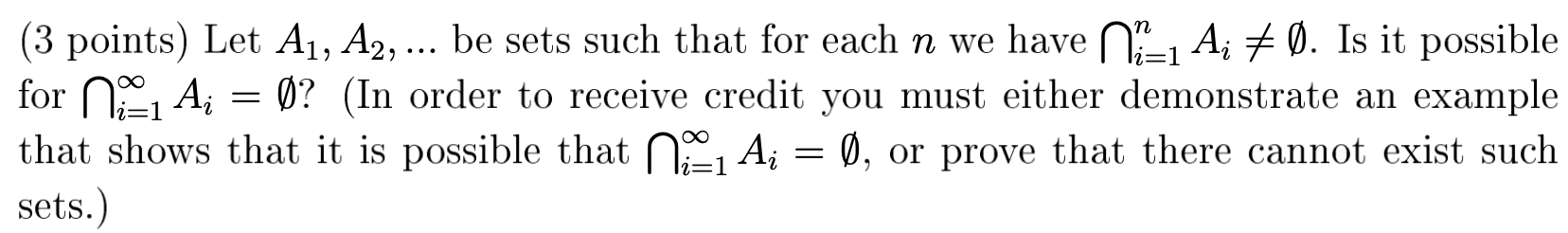
(3 points) Let A1,A2, be sets such that for each n we have i=1nAi=. Is it possible for i=1Ai= ? (In order to receive credit you must either demonstrate an example that shows that it is possible that i=1Ai=, or prove that there cannot exist such sets.)