Question: 3. (Revised 2022-02-01) Define S = [-237, 237]. Let (0, E, P) be a continuous probability space in R3 with probability density function . Define
![3. (Revised 2022-02-01) Define S = [-237, 237]. Let (0, E,](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667a26057ce90_157667a26055450c.jpg)
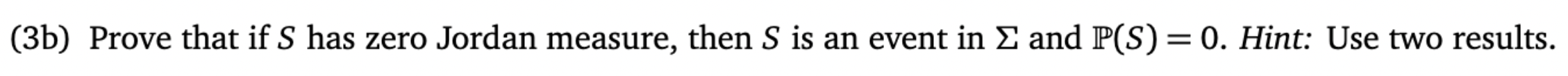
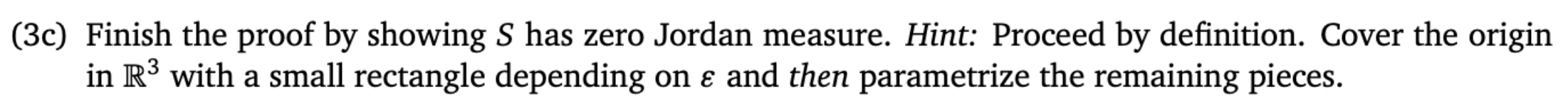
![= 0}. (3a) Choose (A, B, C) E [-237, 237] randomly according](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667a26071ee9c_158667a2606e6260.jpg)
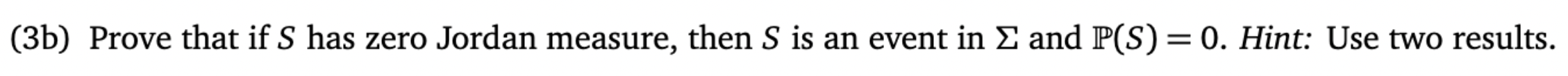
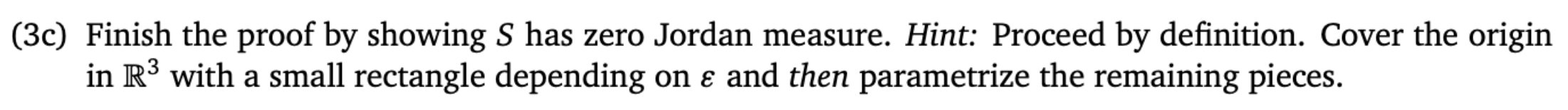
3. (Revised 2022-02-01) Define S = [-237, 237]. Let (0, E, P) be a continuous probability space in R3 with probability density function . Define the set S = {(a, b, c) En: b2 -4ac = 0}. (3a) Choose (A, B, C) E [-237, 237] randomly according to your continuous probability space (n, E, P) and define the quadratic form q : R2 - R by q(x, y) = Ax2 + Bxy + Cy2. Note q has a critical point at (0, 0). Assuming that S is an event in E and P(S) = 0, explain why the second derivative test applied to q at (0, 0) will be conclusive with probability one.(3b) Prove that if S has zero Jordan measure, then S is an event in 2 and 1P(S) = 0. Hint: Use two results. (3c) Finish the proof by showing S has zero Jordan measure. Hint: Proceed by definition. Cover the origin in R3 with a small rectangle depending on & and then parametrizationaining pieces
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


