Question: 3. Simplify. (a) cos A + COS( TT - X) - COS( 7 + x) - cos(-x) (b) tan & + tan( T - x)

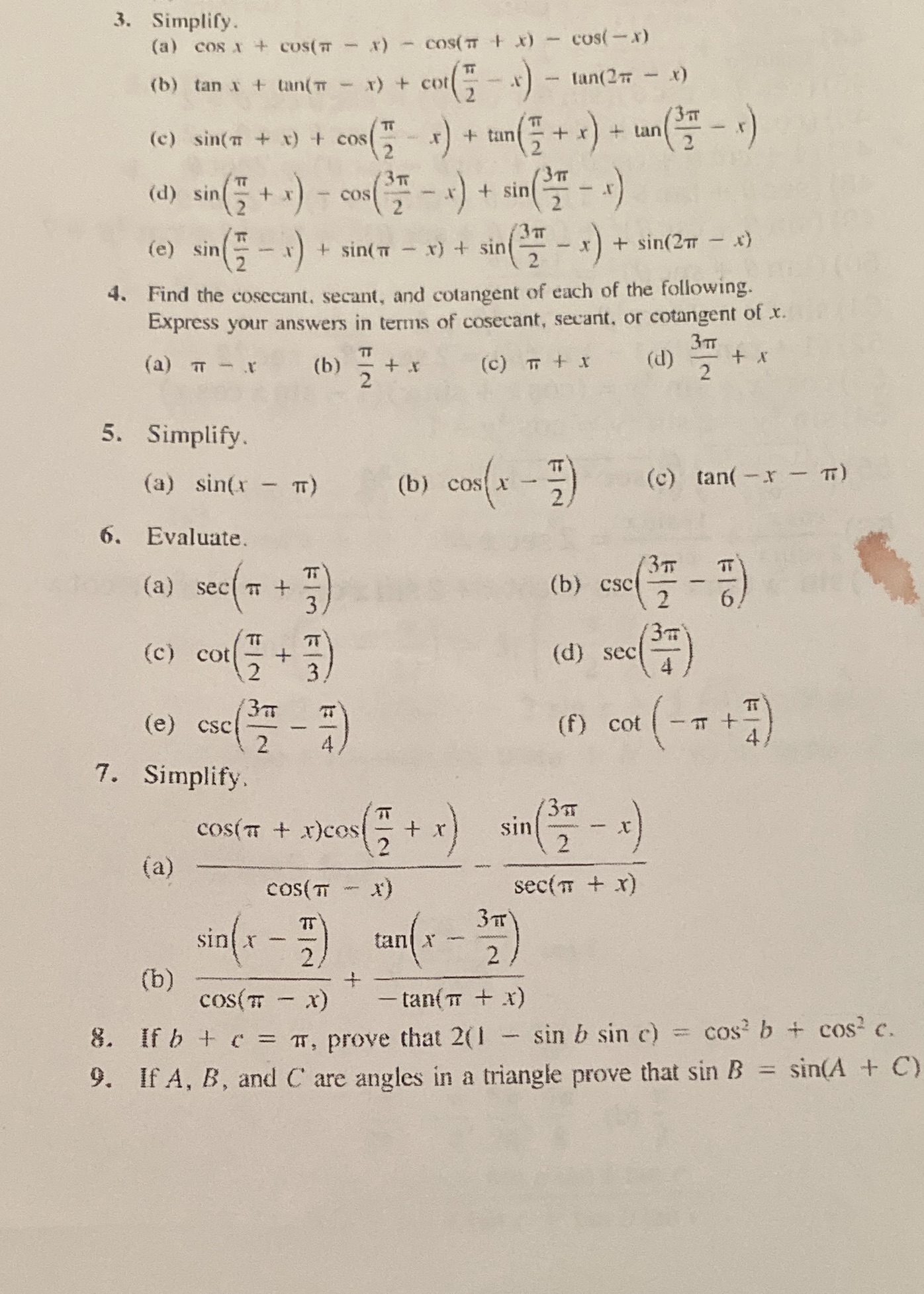
3. Simplify. (a) cos A + COS( TT - X) - COS( 7 + x) - cos(-x) (b) tan & + tan( T - x) + cot(" - x) - lan(27. - x) (c) sin( 7 + x) + cos( -.* ) + ton ( + x ) + can ( 7 - x) + x ) - cos ( " - x ) + sin ( " - x) (e) sin( - x) + sin(T - x) + sin( 7 - x) + sin(2T - x) 4. Find the cosecant. secant, and cotangent of each of the following. Express your answers in terms of cosecant, secant, or cotangent of x. 3TT (a) TT - .x (b) + .x (C) TI + X ( d ) 2 + x 5. Simplify. (a) sin(x - T) (b) cos( x - - (c) tan( - - T) 6. Evaluate. 3TT (a) sec + (b) esc 2 (c) cot TT + (d) sec (e) csc 37 (f) cot - IT + !) 2 4 7. Simplify COS( 7 + x)cos + x) sin 2 (a) COS( TI ~ X) sec( it + x) 3 TT sin x - tan( x 2 (b) + COS( 7 - X) tan( 7 + x) 8. If b + c = 1, prove that 2(1 - sin b sin c) = cos b + cost c. 9. If A, B, and C are angles in a triangle prove that sin B = sin(A + C)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

7/4/23, 11:16 PM Homework 8.7-Anh Nguyen Use a table of integrals to determine tv7t+ 19 at. Click here to view page 1 of the integral table. " Click here to view page 2 of the integral table. 14...

12. [-/1 Points] DETAILS MCKTRIG8 1.4.017. Use the reciprocal identities for the following problem. If tan 0 = a (a # 0), find cot 0. cot 0 = Need Help? Watch It 13. [-/1 Points] DETAILS MCKTRIG8...

(INTEGRAL CALCULUS) Answer the following. Choose only the correct answer from the choices. No need for a detailed solution. In items 15-17 there is no choices so you just have to write the correct...

If you use the fifth Taylor polynomial - sin 3 O (3 5 of f(x) = cos x centered at x = 120 to estimate cos 3 as O - cos 3 (3 -TT) 6 cos 3 = -1 + (3-7) 2 1 720 24 (3 - 7) , O 1 which of the following...

Use the figure and trigonometric identities to find the exact value of the trigonometric function below in two ways B4 4 cos x sin 3 4 cos x sin 3 12 4 cos x sin 3 4 cot 7 2 x sin 7 2 B

One possible way to simplify the trigonometric expression is shown. Choose the correct substitution in each of the steps below from the answer bank provided. Simplify: (secx- cos x). cotx - sin x...

Verify the identity. 1 + Cos x = (csc x + cotx)2 1 - cos x To verify the identity, start with the more complicated side and transform it to look like the other side. Choose the correct...

1 2 4 6 P 14 8 R Directions Solve for x Round to the nearest tenth 3 17 48 29 22 50 37 48 X 12 l 58 5 X 16 7 9 sino COQ tan O 37 24 29 67 9 15 51 x sin R cos R tan R

a Write the integral that gives the area of the surface generated when the curve is revolved about the given axis b Use a calculator or software to approximate the surface area y 2 cos x for 0 x...

Please help me answering these questions. 1, \fFind the inverse function f* of the function f. f(x) = - 7 cos (9x) O A. f 1 (x) = = cos ' ( ") OB. F (x) = - 7 cos (9x) Oc. f ( x) = ac 7 OD. f 1 (x) =...

As bad as the continuing supply chain crisis is for many organizations, some companies have found ways to meet and beat the challenges. On Wednesday, for example, the Wall Street Journal reported...

Some people choose to live close to the city center; others choose to live away from the city and take a longer commute to work every day. Does picking a location with a longer commute imply a...

The direct labor rate variance in the direct labor standard costing model is the responsibility of the human resources department.

Need help with solving this problem using simple python code steps. 2.) A jet's position on an aircraft carrier's runway was timed during landing to produce the following data: t (seconds) 0 0.52 1.04