3.1 The Tukey Honestly Significant Difference Procedure

The problem with performing inferences on all pairs of means, as we have done above, is that it lends itself to data snooping, i.e., looking for the mean differences that we did not necessarily hypothesize a priori. Tukey's HSD procedure tries to correct for that problem by adjusting critical values for the fact that we are first looking for the biggest observed difference in the analysis. Tukey's procedure is appropriate if you plan to compare all pairs of means. If you only plan to compare a small subset of the pairs, then the Tukey procedure can be overly conservative. To perform Tukey's HSD check off the "Tukey" box under the "Post Hoc Tests for" options in the general linear model procedure.

Task 7.Reportthe Tukey confidence intervals and p-values and compare the Tukey confidence intervals and p-values to the unadjusted ones (LSD). Which confidence intervals are wider?

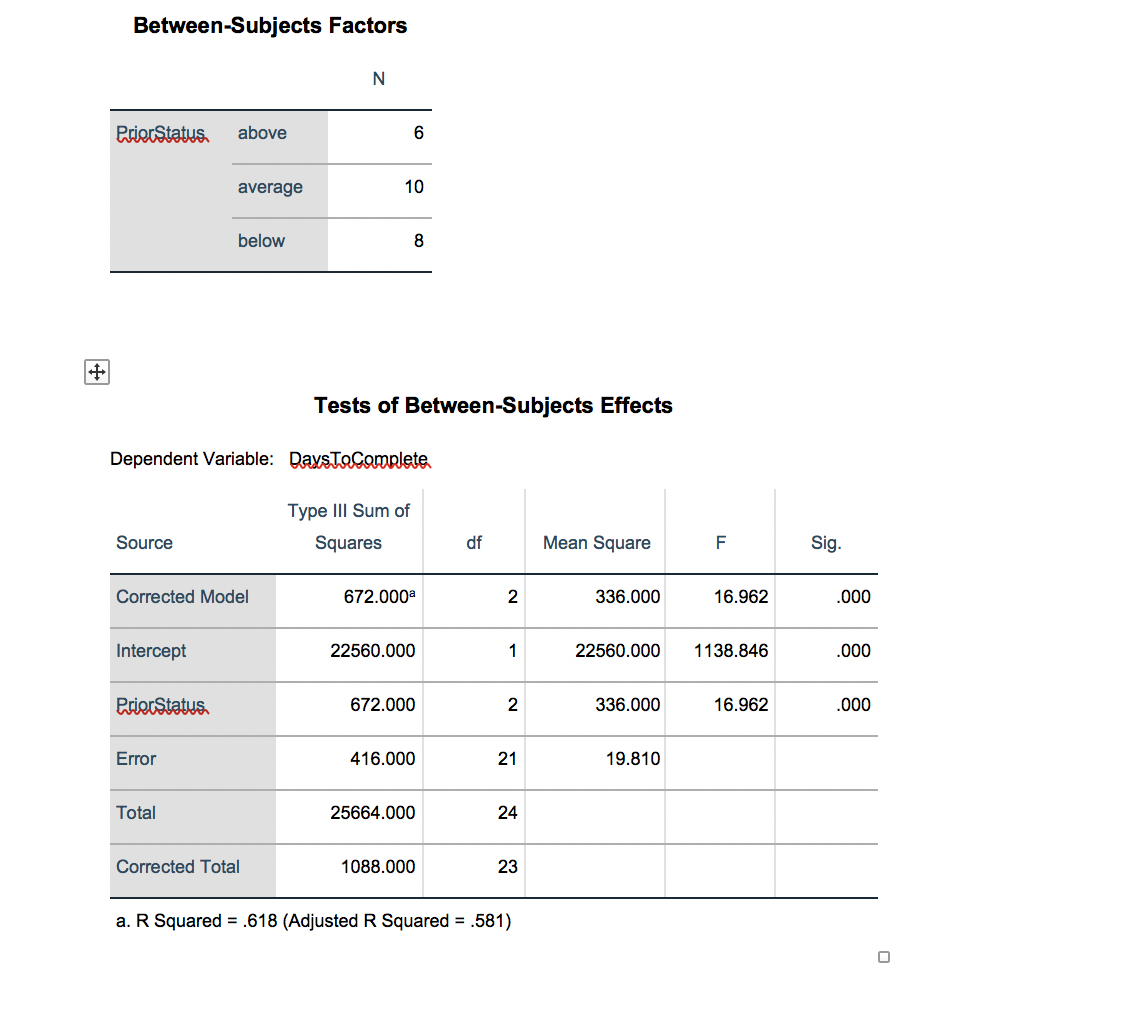
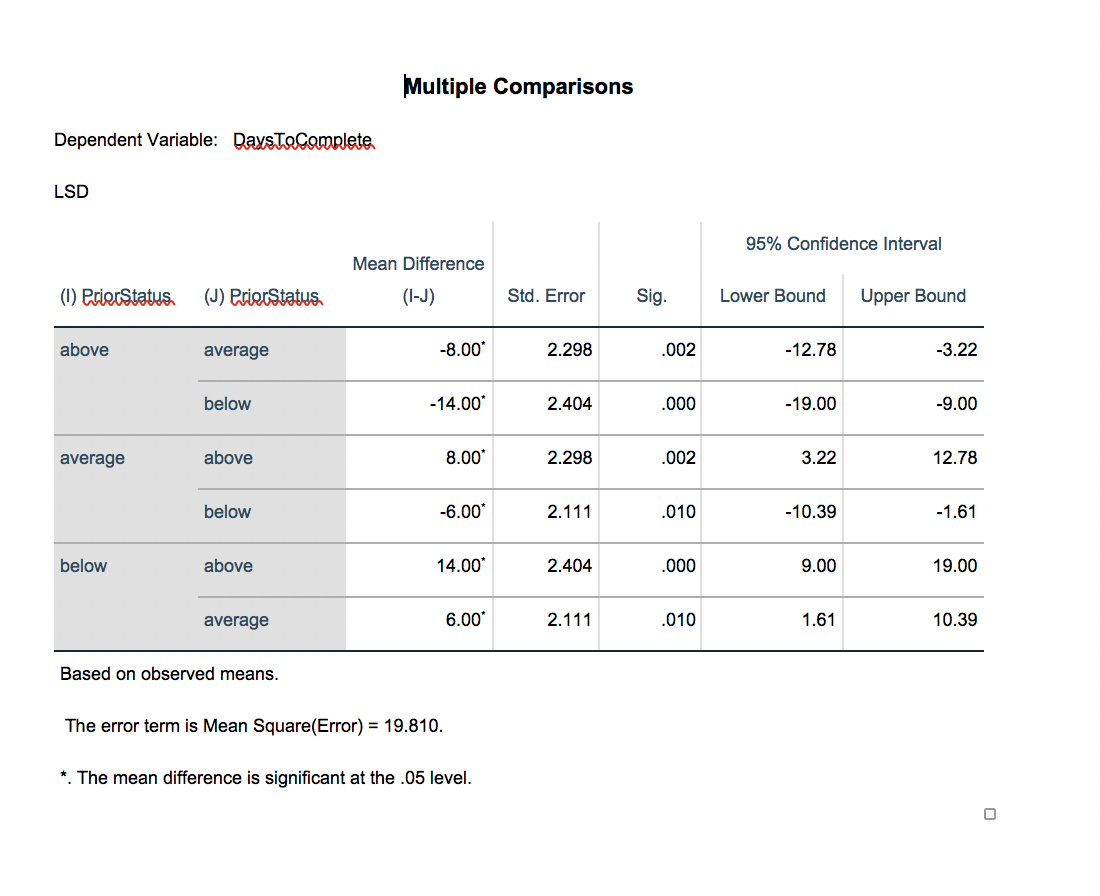
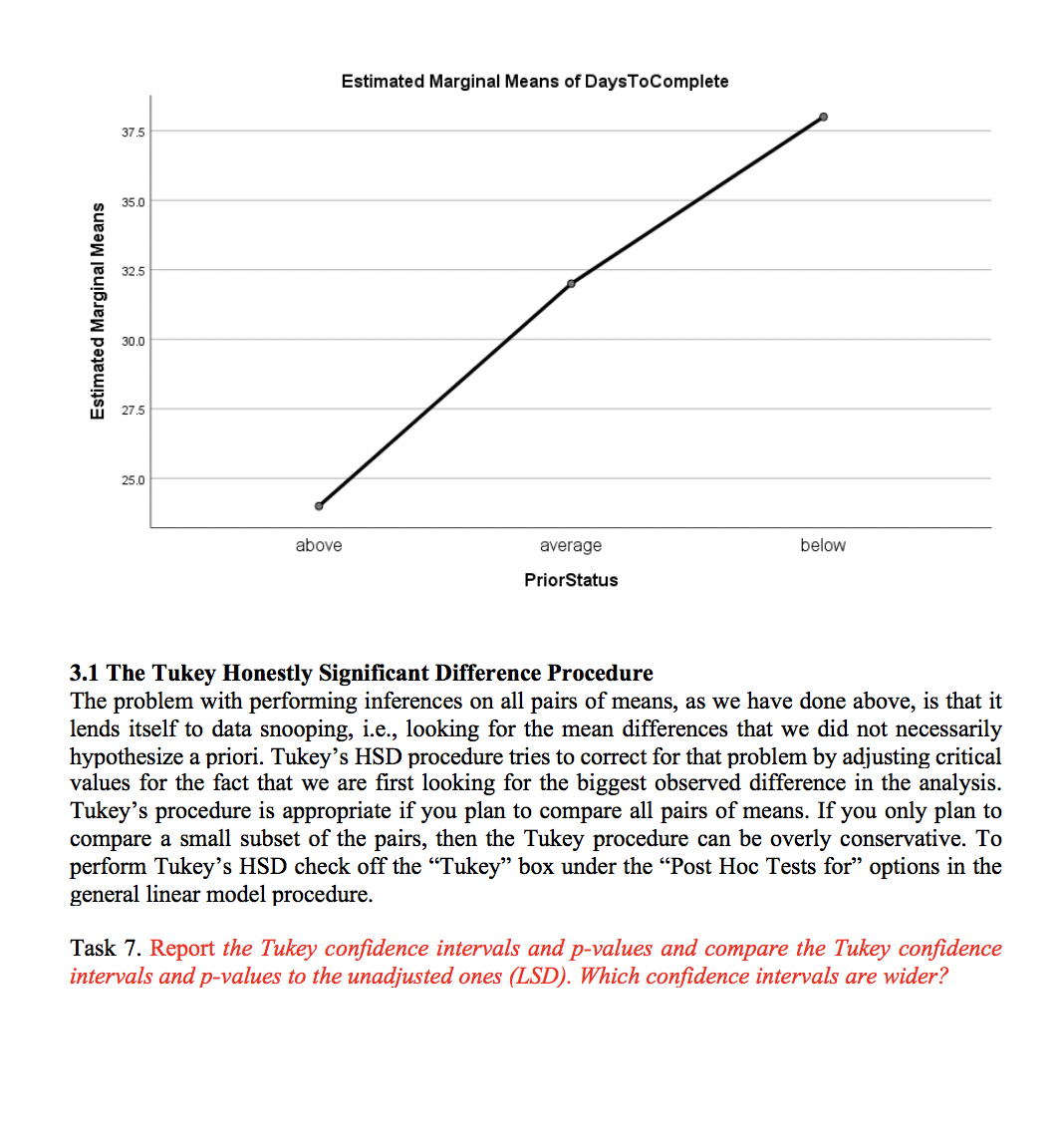
Between-Subjects Factors N moms. above 5 average 1 0 below 8 Tests of Between-Subjects Effects Dependent Variable: mm Type III Sum of Source Squares Corrected Model 6]'2.000a Intercept 22560.000 3mm 672.000 Error 416.000 Total 25664.000 Corrected Total 1088.000 21 24 23 a. R Squared = .618 (Adjusted R Squared = .581) Mean Square 336.000 22560.000 336.000 19.810 16.962 1138.846 16.962 Sig. .000 .000 .000 Multiple Comparisons Dependent Variable: mm LSD 0) 3m above average below Based on observed means. (J) 351mm average below above below above average Mean Difference (l-J) Std. Error -8.00' 2.298 -14.00' 2.404 8.00' 2.298 -6.00' 2.1 1 1 14.00' 2.404 6.00' 2.1 1 1 The error term is Mean Square(Error) = 19.810. *. The mean difference is signicant at the .05 level. Sig. .002 .000 .002 .010 .000 .010 95% Condence Interval Lower Bound Upper Bound -12.78 -3.22 -19.00 -9.00 3.22 12.78 -10.39 -1.61 9.00 19.00 1.61 10.39 Estimated Marginal Means of Days ToComplete 37.5 Estimated Marginal Means 35.0 32.5 30.0 27.5 25.0 above average below PriorStatus 3.1 The Tukey Honestly Significant Difference Procedure The problem with performing inferences on all pairs of means, as we have done above, is that it lends itself to data snooping, i.e., looking for the mean differences that we did not necessarily hypothesize a priori. Tukey's HSD procedure tries to correct for that problem by adjusting critical values for the fact that we are first looking for the biggest observed difference in the analysis Tukey's procedure is appropriate if you plan to compare all pairs of means. If you only plan to compare a small subset of the pairs, then the Tukey procedure can be overly conservative. To perform Tukey's HSD check off the "Tukey" box under the "Post Hoc Tests for" options in the general linear model procedure. Task 7. Report the Tukey confidence intervals and p-values and compare the Tukey confidence intervals and p-values to the unadjusted ones (LSD). Which confidence intervals are wider